题目内容
19.椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)与双曲线$\frac{{x}^{2}}{b}$-y2=1(b>0)有相同的焦点F1,F2,若P为两曲线的一个交点,则△PF1F2的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意,设P的坐标为(m,n),则有$\left\{\begin{array}{l}{\frac{{m}^{2}}{a}+{n}^{2}=1}\\{\frac{{m}^{2}}{b}-{n}^{2}=1}\end{array}\right.$,解可得m、n的值,可以表示△PF1F2的面积S,又由椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)与双曲线$\frac{{x}^{2}}{b}$-y2=1(b>0)有相同的焦点,分析可得a-1=b+1,即b=a-2,代入S中,计算可得答案.
解答 解:根据题意,设两曲线的一个交点P的坐标为(m,n),
则有$\left\{\begin{array}{l}{\frac{{m}^{2}}{a}+{n}^{2}=1}\\{\frac{{m}^{2}}{b}-{n}^{2}=1}\end{array}\right.$,解可得$\left\{\begin{array}{l}{m=±\sqrt{\frac{2ab}{a+b}}}\\{n=±\sqrt{\frac{a-b}{a+b}}}\end{array}\right.$,
椭圆圆$\frac{{x}^{2}}{a}$+y2=1中,|F1F2|=2c=2$\sqrt{a-1}$,
△PF1F2的面积S=$\frac{1}{2}$×|n|×2$\sqrt{a-1}$=$\sqrt{\frac{a-b}{a+b}}$×$\sqrt{a-1}$,
又由椭圆$\frac{{x}^{2}}{a}$+y2=1(a>1)与双曲线$\frac{{x}^{2}}{b}$-y2=1(b>0)有相同的焦点,
则有a-1=b+1,即b=a-2,
则S=$\sqrt{\frac{2}{2a-2}}$×$\sqrt{a-1}$=1;
故选:A.
点评 本题考查椭圆、双曲线的几何性质,注意两曲线的焦点相同,构造a、b的关系.

 应用题作业本系列答案
应用题作业本系列答案| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{10}$ |
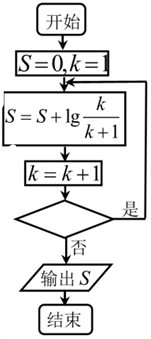
| A. | k≤8 | B. | k≤9 | C. | k≤10 | D. | k≤11 |
| A. | [$\frac{ln3}{3}$,$\frac{1}{e}$) | B. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | C. | (0,$\frac{1}{e}$) | D. | (0,$\frac{1}{2e}$) |
 一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?
一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示.ABCD是等腰梯形,AB=20米,∠CBF=α(F在AB的延长线上,α为锐角).圆E与AD,BC都相切,且其半径长为100-80sinα米.EO是垂直于AB的一个立柱,则当sinα的值设计为多少时,立柱EO最矮?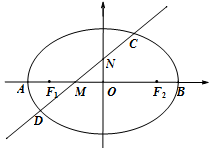 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,|AB|=4,|F1F2|=2$\sqrt{3}$,直线l:y=kx+m(k>0)交椭圆于C、D两点,与线段F1F2及椭圆短轴分别交于M、N两点(M、N不重合),且|CM|=|DN|.