题目内容
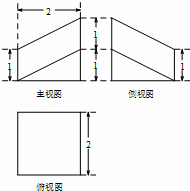
如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点E是棱AB上的动点.
(Ⅰ)求证:DA1⊥ED1;
(Ⅱ)若直线DA1与平面CED1成角为45°,求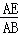 的值;
的值;
(Ⅲ)写出点E到直线D1C距离的最大值及此时点E的位置(结论不要求证明).
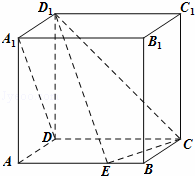
【解析】以D为坐标原点,建立如图所示的坐标系,则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D1(0,1,2),A1(1,0,1),设E(1,m,0)(0≤m≤1)
(Ⅰ)证明: =(1,0,1),
=(1,0,1), =(﹣1,﹣m,1)
=(﹣1,﹣m,1)
∴ •
• =0
=0
∴DA1⊥ED1;(4分)
(Ⅱ)解:设平面CED1的一个法向量为 =(x,y,z),则
=(x,y,z),则
∵ =(0,﹣1,1),
=(0,﹣1,1), =(1,m﹣1,0)
=(1,m﹣1,0)
∴ .
.
取z=1,得y=1,x=1﹣m,得 =(1﹣m,1,1).
=(1﹣m,1,1).
∵直线DA1与平面CED1成角为45°,
∴sin45°=|cos< ,
, >|=
>|= ,
,
∴ =
= ,解得m=
,解得m= .﹣﹣﹣﹣﹣(11分)
.﹣﹣﹣﹣﹣(11分)
(Ⅲ)解:点E到直线D1C距离的最大值为 ,此时点E在A点处.﹣﹣﹣﹣﹣﹣(14分)
,此时点E在A点处.﹣﹣﹣﹣﹣﹣(14分)


练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 取余法”将十进制数
取余法”将十进制数 转化为五进制数是( )
转化为五进制数是( ) .
.
 .
.
 .
.
 .
.
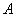 样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若
样本数据如下:82, 84, 84, 86, 86, 86, 88, 88, 88, 88.若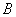 样本数据恰好是
样本数据恰好是 上任一点
上任一点 处切线斜率为
处切线斜率为 ,则函数
,则函数 的部分图象可以为.
的部分图象可以为.
 的实部是 ( )
的实部是 ( ) 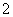 B.
B.  C.
C. D.
D.
 向左平移
向左平移 个单位后,得到函数
个单位后,得到函数 ,下列关于
,下列关于 中心对称 B.图象关于
中心对称 B.图象关于 轴对称
轴对称 单调递增 D.在
单调递增 D.在 单调递减
单调递减