题目内容
9．若某程序框图如图所示，则该程序运行后输出的值等于5
分析 根据已知流程图可得程序的功能是计算并输出S=log23×log34×…×log3132的值，利用换底公式易得答案．
解答 解：模拟执行程序，根据框图流程，可得
S=1，k=2
不满足条件k＞31，执行循环体，S=log23，k=3
不满足条件k＞31，执行循环体，S=log23×log34，k=4
…
不满足条件k＞31，执行循环体，S=log23×log34×…×log3132，k=32
满足条件k＞31，退出循环，输出S=log23×log34×…×log3132=$\frac{lg3}{lg2}$×$\frac{lg4}{lg3}$×…×$\frac{lg32}{lg31}$=$\frac{lg32}{lg2}$=5．
故答案为：5．
点评 本题考查的知识点是程序框图的应用，其中分析出程序的功能是解答的关键．同时考查了阅读框图的能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．设函数f（x）=cos（2x+$\frac{π}{4}$）+sin（2x+$\frac{π}{4}$），则（ ）
| A． | 函数f（x）在区间（$\frac{π}{2}，π$）内单调递增，其图象关于直线x=$\frac{π}{4}$对称 | |
| B． | 函数f（x）在区间（$\frac{π}{2}$，π）内单调递增，其图象关于直线x=$\frac{π}{2}$对称 | |
| C． | 函数f（x）在区间（$\frac{π}{2}$，π）内单调递减，其图象关于直线x=$\frac{π}{4}$对称 | |
| D． | 函数f（x）在区间（$\frac{π}{2}，π$）内单调递减，其图象关于直线x=$\frac{π}{2}$对称 |
20．下列函数：①y=-$\frac{1}{x+1}$；②y=（x-1）3；y=log2x-1；④y=-（$\frac{1}{2}$）|x|中，在（0，+∞）上是增函数且不存在零点的函数的序号是（ ）
| A． | ①④ | B． | ②③ | C． | ②④ | D． | ①③④ |
4．执行如图所示的程序框图，如果输入的N=2016，那么输出的S=（ ）
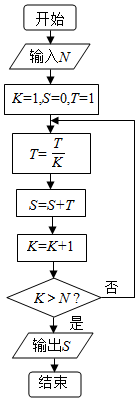
| A． | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$ | B． | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2015!}$ | ||
| C． | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2016}$ | D． | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$ |
14．i（1-$\sqrt{3}$i）等于（ ）
| A． | $\sqrt{3}$-i | B． | $\sqrt{3}$+i | C． | -$\sqrt{3}$-i | D． | -$\sqrt{3}$+i |