题目内容
9.已知平面向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,5),$\overrightarrow{c}$=(m,3),且($\overrightarrow{a}$+$\overrightarrow{c}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$),则m=$\frac{3±\sqrt{17}}{2}$.分析 根据平面向量的坐标运算与共线定理,列出方程求出m的值.
解答 解:平面向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(2,5),$\overrightarrow{c}$=(m,3),
则$\overrightarrow{a}$+$\overrightarrow{c}$=(1+m,m+3),
$\overrightarrow{a}$-$\overrightarrow{b}$=(-1m-5),
且($\overrightarrow{a}$+$\overrightarrow{c}$)∥($\overrightarrow{a}$-$\overrightarrow{b}$),
∴(1+m)(m-5)+(m+3)=0,
m2-3m-2=0,
解得m=$\frac{3+\sqrt{17}}{2}$或m=$\frac{3-\sqrt{17}}{2}$.
故答案为:$\frac{{3±\sqrt{17}}}{2}$.
点评 本题考查了平面向量的坐标运算与共线定理应用问题,是基础题目.

练习册系列答案
相关题目
20.若a,b∈R且ab≠0,则$\frac{1}{a^2}>\frac{1}{b^2}$成立的一个充分非必要条件是( )
| A. | a>b>0 | B. | b>a | C. | a<b<0 | D. | ab(a-b)<0 |
17.已知$tanα=-\frac{3}{4}$,则sinα(sinα-cosα)=( )
| A. | $\frac{21}{25}$ | B. | $\frac{25}{21}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
18.已知{an}是等差数列,且公差d≠0,Sn为其前n项和,且S5=S6,则S11=( )
| A. | 0 | B. | 1 | C. | 6 | D. | 11 |
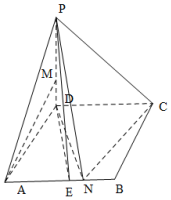 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=3,PM=2MD,AN=2NB,
 如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=0,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点.
如图,已知菱形ABCD的边长为6,∠BAD=60°,AC∩BD=0,将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点.