题目内容
16．已知双曲线的左右焦点分别为F1，F2，过F2的直线与右支交于A，B两点，若|AB|=5，且实轴长为8，则△ABF1的周长是26．分析 根据双曲线的定义和性质，即可求出三角形的周长．
解答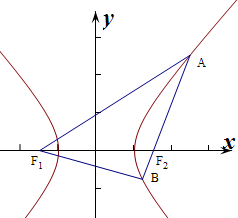 
解：由题意可知a=4，
则|AF1|-|AF2|=8，|BF1|-|BF2|=8，
则|AF1|+|BF1|-（|BF2|+|AF2|）=16，
即|AF1|+|BF1|=|BF2|+|AF2|+16=|AB|+16=5+16=21，
则△ABF1的周长为|AF1|+|BF1|+|AB|=21+5=26，
故答案为：26．
点评 本题主要考查双曲线的定义，根据双曲线的定义得到A，B到两焦点距离之差是个常数是解决本题的关键．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
7．曲线C以双曲线$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{2}$=1的右焦点F为焦点，曲线C上的点到焦点F的距离与到直线x=-2的距离相等，则曲线C上的任意一点P到y轴的距离与到直线x-y+4=0的距离和的最小值为（ ）
| A． | 3$\sqrt{2}$ | B． | 3$\sqrt{2}$-1 | C． | 3$\sqrt{2}$+2 | D． | 3$\sqrt{2}$-2 |
4．已知函数y=-x2+3x，直线l1：x=t和l2：x=t+1（其中0≤t≤2，t为常数），若直线l1，l2，x轴与函数y=f（x）的图象所围成的封闭图形的面积为S，则S的最大值为（ ）
| A． | 2 | B． | $\frac{11}{6}$ | C． | $\frac{13}{6}$ | D． | 3 |
6．下列说法中，正确的是（ ）
| A． | 命题“若am2＜bm2，则a＜b”的逆命题是真命题 | |
| B． | 命题“存在x∈R，x2-x＞0”的否定是：“任意x∈R，x2-x≤0” | |
| C． | 命题“p或q”为真命题，则命题“p”和命题“q”均为真命题 | |
| D． | 已知x∈R，则“x＞1”是“x＞2”的充分不必要条件 |