题目内容
1.已知函数f(x)=$\frac{2x-a}{x-2a}$.a∈R(1)若1∈{x|f(x)>1},求a的取值范围.
(2)解不等式f(x)>1,用含a的代数式表示不等式的解集.
分析 (1)若1∈{x|f(x)>1},则由f(1)>1,即可求a的取值范围.
(2)根据分式不等式的性质,将不等式转化为一元二次不等式,讨论参数a的取值范围即可得到结论.
解答 解:(1)若1∈{x|f(x)>1},则f(x)>1,
即$\frac{2-a}{1-2a}$>1,
即$\frac{a-2}{2a-1}$>1,
则$\frac{a-2}{2a-1}$-1=$\frac{-a-1}{2a-1}$>0,
即$\frac{a+1}{2a-1}$<0,
解得-1<a<$\frac{1}{2}$,
即a的取值范围是-1<a<$\frac{1}{2}$.
(2)由f(x)>1,得$\frac{2x-a}{x-2a}$>1,即$\frac{2x-a}{x-2a}$-1=$\frac{x+a}{x-2a}$>0,
即(x+a)(x-2a)>0,
若a=0,则不等式等价为x2>0,则x≠0,
若a>0,则不等式的解为x>2a或x<-a,
若a<0,则不等式的解为x>-a或x<2a,
综上若a=0,则不等式的解集为{x|x≠0},
若a>0,则不等式的解集为{x|x>2a或x<-a},
若a<0,则不等式的解集为{x|x>-a或x<2a}.
点评 本题主要考查不等式的求解,根据分式不等式的解法转化为一元二次不等式是解决本题的关键.

练习册系列答案
相关题目
12.对于大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”:23=3+5,33=7+9+11,43=13+15+17+19,…,仿此,若m3的“分裂数”中有一个是61,则m的值是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
11.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积是( )
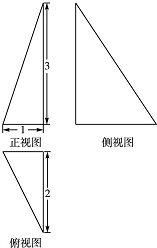

| A. | 1 m3 | B. | 2 cm3 | C. | 3 cm3 | D. | 6 cm3 |