题目内容
2.某单位为了了解办公楼用电量y(度)与气温x(℃)之间的关系,随机统计了四个工作日的用电量与当天平均气温,并制作了对照表:| 气温(℃) | 17 | 14 | 11 | -2 |
| 用电量(度) | 23 | 35 | 39 | 63 |
| A. | 38度 | B. | 50度 | C. | 70度 | D. | 30度 |
分析 由表中数据计算$\overline{x}$、$\overline{y}$,代入线性回归方程中求出a的值,
写出回归方程,利用方程求出x=-5时$\stackrel{∧}{y}$的值.
解答 解:由表中数据计算$\overline{x}$=$\frac{1}{4}$×(17+14+11-2)=10,
$\overline{y}$=$\frac{1}{4}$×(23+35+39+63)=40,
代入线性回归方程$\stackrel{∧}{y}$=-2x+a中,
计算a=$\overline{y}$+2$\overline{x}$=40+2×10=60,
∴回归方程为$\stackrel{∧}{y}$=-2x+60;
当x=-5时,$\stackrel{∧}{y}$=-2×(-5)+60=70,
即气温为-5℃时预测用电量约为70度.
故选:C.
点评 本题考查了线性回归方程的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知{an}为等比数列,a4+a7=2,a2a9=-8,则a1+a10=( )
| A. | 7 | B. | 5 | C. | -7 | D. | -5 |
17.已知m∈N*,则乘积m(m+1)(m+2)…(m+15)可表示为( )
| A. | A${\;}_{m}^{15}$ | B. | A${\;}_{m}^{16}$ | C. | A${\;}_{m+15}^{15}$ | D. | A${\;}_{m+15}^{16}$ |
7.如图,在△OBC中,点A是BC的中点,$\overrightarrow{OD}$=2$\overrightarrow{DB}$,DC和OA交于点E,则AO与OE的比值为( )

| A. | $\frac{6}{5}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | 2 |
14.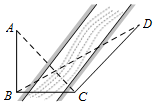 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
 如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )
如图,某人为测量河对岸塔AB的高,先在塔底B的正东方向上的河岸上选一点C,在点C处测得点A的仰角为45°,并在点C北偏东15°方向的河岸上选定一点D,测得CD的距离为20米,∠BDC=30°,则塔AB的高是( )| A. | 10米 | B. | $10\sqrt{2}$米 | C. | $10\sqrt{3}$米 | D. | $20\sqrt{3}$米 |
15.△ABC中,若a:b=cosA:cosB,则△ABC是( )
| A. | 直角三角形 | B. | 等边三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |