题目内容
在△ABC中,内角A.B.C依次成等差数列,AB=8,BC=5,则△ABC内切圆的面积是( )
A、
| ||
| B、3π | ||
| C、6π | ||
| D、12π |
考点:正弦定理
专题:解三角形
分析:先根据三个内角成等差数列求得B,进而利用余弦定理求得AC,根据AB,BC和sinB求得三角形的面积,然后根据S△ABC=
(AB+BC+AC)•r求得内切圆的半径,最后利用圆的面积公式求得答案.
| 1 |
| 2 |
解答:
解:依题意2B=A+C,
∴A+C+B=3B=180°,
∴B=60°,
AC=
=7,
S△ABC=
AB•BC•sinB=
×8×5×
=10
,
设三角形内切圆半径为r,
S△ABC=
(AB+BC+AC)•r=
×20•r=10
,
∴r=
,
∴内切圆的面积为πr2=3π,
故选:B.
∴A+C+B=3B=180°,
∴B=60°,
AC=
| AB2+BC2-2AB•BC•cosB |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
设三角形内切圆半径为r,
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∴r=
| 3 |
∴内切圆的面积为πr2=3π,
故选:B.
点评:本题主要考查了正弦定理和余弦定理的应用.在解三角形问题中要合理运用公式求解边,面积和外接圆半径等,属于基础题.

练习册系列答案
相关题目
若函数f(x)为奇函数,且在(0,+∞)上是减函数,又f(3)=0,则
<0的解集为( )
| f(x)-f(-x) |
| x |
| A、(-3,3) |
| B、(-∞,-3)∪(0,3) |
| C、(-3,0)∪(3,+∞) |
| D、(-∞,-3)∪(3,+∞) |
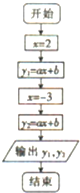 如图是为解决某个问题而绘制的程序框图,仔细分析各图框内的内容及框图之间的关系,回答下面的问题:
如图是为解决某个问题而绘制的程序框图,仔细分析各图框内的内容及框图之间的关系,回答下面的问题: