题目内容
设函数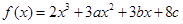 在
在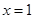 及
及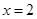 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)当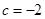 时,求函数
时,求函数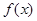 在区间
在区间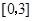 上的最大值.
上的最大值.
【答案】
①解:  ,
,
因为函数 在
在 及
及 取得极值,则有
取得极值,则有 ,
, .
.
即
解得 ,
, .Zxxk
.Zxxk
②由(Ⅰ)可知, ,
,
 .
.
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, .
.
所以,当 时,
时, 取得极大值
取得极大值 ,又
,又 ,
, .
.
则当 时,
时, 的最大值为
的最大值为 .
.
【解析】略

练习册系列答案
相关题目
 在
在 及
及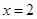 时取得极值.
时取得极值. ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围. 在
在 及
及 时取得极值.
时取得极值. ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.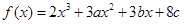 在
在 及
及 时取得极值.
时取得极值. 、b的值;
、b的值; ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.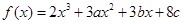 在
在 及
及 时取得极值;
时取得极值; 与b的值;
与b的值; ,都有
,都有 成立,求c的取值范围。
成立,求c的取值范围。