题目内容
设函数 在
在 及
及 时取得极值.
时取得极值.
(1)求a、b的值;(2)若对于任意的 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.
【答案】
(1) ,
, ;(2)
;(2)
【解析】
试题分析:(1)由函数 ,可得
,可得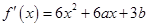 ,又函数
,又函数 在
在 与
与 处取得极值,所以
处取得极值,所以 ,即
,即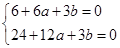 ,从而解得
,从而解得 ,
, .
.
(2)由(1)可得 ,则
,则 ,
,
|
|
0 |
|
1 |
|
2 |
|
3 |
|
|
+ |
+ |
0 |
- |
- |
+ |
+ |
|
|
|
增函数 |
极大值
|
减函数 |
极小值
|
增函数 |
|
由上表可得函数 在
在 上的最大值为
上的最大值为 ,又对于任意的
,又对于任意的 都有
都有 成立,所以
成立,所以 ,从而可求出
,从而可求出 的取值范围为
的取值范围为 .
.
试题解析:(1) ,
,
因为函数 在
在 及
及 取得极值,则有
取得极值,则有 ,
, .
.
即
解得 ,
, .
.
(2)由(Ⅰ)可知,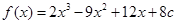 ,
,
 .
.
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, .
.
所以,当 时,
时, 取得极大值
取得极大值 ,又
,又 ,
, .
.
则当 时,
时, 的最大值为
的最大值为 .
.
因为对于任意的 ,有
,有 恒成立,
恒成立,
所以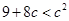 ,
,
解得 或
或 ,
,
因此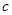 的取值范围为
的取值范围为 .
.
考点:1.导数;2.函数的极值、最值.

练习册系列答案
相关题目








 在
在 及
及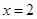 时取得极值.
时取得极值. ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.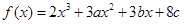 在
在 及
及 时取得极值.
时取得极值. 、b的值;
、b的值; ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.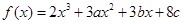 在
在 及
及 时取得极值;
时取得极值; 与b的值;
与b的值; ,都有
,都有 成立,求c的取值范围。
成立,求c的取值范围。