题目内容
不等式|
+2|>
的解集为
| 1 | ||
log
|
| 3 |
| 2 |
(0,1)∪(1,2
)∪(4,+∞)
| 2 |
| 7 |
(0,1)∪(1,2
)∪(4,+∞)
.| 2 |
| 7 |
分析:根据绝对值不等式的性质,先去绝对值,然后解分式不等式以及对数不等式,注意对数的真数大于0.
解答:解:|
+2|>
等价于
+2>
或
+2<-
.
即
>-
或
<-
.
此时log
x<-2或log
x>0或-
<log
x<0.
∴解为x>4或0<x<1 或 1<x<2
.
即解集为(0,1)∪(1,2
)∪(4,+∞).
故答案为:(0,1)∪(1,2
)∪(4,+∞).
| 1 | ||
log
|
| 3 |
| 2 |
| 1 | ||
log
|
| 3 |
| 2 |
| 1 | ||
log
|
| 3 |
| 2 |
即
| 1 | ||
log
|
| 1 |
| 2 |
| 1 | ||
log
|
| 7 |
| 2 |
此时log
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 7 |
| 1 |
| 2 |
∴解为x>4或0<x<1 或 1<x<2
| 2 |
| 7 |
即解集为(0,1)∪(1,2
| 2 |
| 7 |
故答案为:(0,1)∪(1,2
| 2 |
| 7 |
点评:本题主要考查了绝对值不等式,以及分式不等式和对数不等式,解题时需注意对数函数的定义域,属于基础题.

练习册系列答案
相关题目
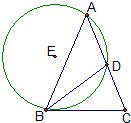 (1)如图,在△ABC中,AB=AC,∠C=72°,⊙E过A,B两点且与BC相切于点B,与AC交于点D,连接BD,若
(1)如图,在△ABC中,AB=AC,∠C=72°,⊙E过A,B两点且与BC相切于点B,与AC交于点D,连接BD,若