题目内容
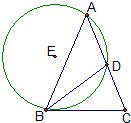 (1)如图,在△ABC中,AB=AC,∠C=72°,⊙E过A,B两点且与BC相切于点B,与AC交于点D,连接BD,若BC=
(1)如图,在△ABC中,AB=AC,∠C=72°,⊙E过A,B两点且与BC相切于点B,与AC交于点D,连接BD,若BC=| 5 |
(2)过点A(2,3)的直线的参数方程为
|
(3)若关于x的不等式x+|x-1|≤a无解,则实数a的取值范围为
分析:(1)平面几何中的问题,借助圆中等角所对的弦长相等
(2)将直线的参数的参数方程化为普通方程,联立求解得点B的坐标、
(3)绝对值不等式的恒成立问题,讨论去绝对值符号,然后求解
(2)将直线的参数的参数方程化为普通方程,联立求解得点B的坐标、
(3)绝对值不等式的恒成立问题,讨论去绝对值符号,然后求解
解答:(1)解:由已知得BD=AD=BC,BC2=CD•AC=(AC-BC)•AC,得AC=2,
(2)解析:2
由
得2x-y-1=0,
解方程组
得点B(4,7),|AB|=
=2
.
(3)解析:设f(x)=x+|x-1|,
则f(x)=
故f(x)的最小值为1
则x+|x-1|≤1无解,
故a<1时,f(x)≤a无解.
(2)解析:2
| 5 |
|
解方程组
|
得点B(4,7),|AB|=
| (4-2)2+(7-3)2 |
| 5 |
(3)解析:设f(x)=x+|x-1|,
则f(x)=
|
故f(x)的最小值为1
则x+|x-1|≤1无解,
故a<1时,f(x)≤a无解.
点评:(1)圆中同弧所对的圆周角相等,等角所对的弦长相等
(2)参数方程与普通方程的互化、两点间距离公式
(3)解决绝对值不等式的关键就是去绝对值符号
(2)参数方程与普通方程的互化、两点间距离公式
(3)解决绝对值不等式的关键就是去绝对值符号

练习册系列答案
相关题目
 14、矩形ABCD中,对角线AC与边AB、AD所成的角分别为a、b,则cos2a+cos2b=1.如图,在长方体ABCD-A1B1C1D1中,请应用类比推理,写出一个类似的结论:
14、矩形ABCD中,对角线AC与边AB、AD所成的角分别为a、b,则cos2a+cos2b=1.如图,在长方体ABCD-A1B1C1D1中,请应用类比推理,写出一个类似的结论: 通常用a、b、c分别表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC的外接圆半径.
通常用a、b、c分别表示△ABC的三个内角A,B,C所对边的边长,R表示△ABC的外接圆半径. (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. 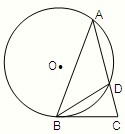 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.