��Ŀ����
14����֪��ԲC�ķ���Ϊ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}����{F_1}��{F_2}$Ϊ�����ҽ��㣬eΪ�����ʣ�PΪ��Բ��һ���㣬��������˵�����ٵ�0��e��$\frac{{\sqrt{2}}}{2}$ʱ��ʹ��PF1F2Ϊֱ�������εĵ�P����ֻ��4����
�ڵ�e=$\frac{{\sqrt{2}}}{2}$ʱ��ʹ��PF1F2Ϊֱ�������εĵ�P����ֻ��6����
�۵�$\frac{{\sqrt{2}}}{2}$��e��1ʱ��ʹ��PF1F2Ϊֱ�������εĵ�P����ֻ��8����
����˵������ȷ�ĸ����ǣ�������
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ������Բ�������ʵ�ȡֵ��Χ���ó���Բ�Ķ���Ķ��㹹�ɵĽǡ�F1BF2��ȡֵ��Χ���ֱ��жϣ�ʹ��PF1F2Ϊֱ�������εĵ�P������
��� 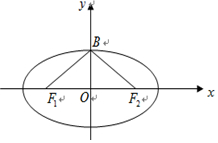 �⣺��ͼ��ʾ��حBF1ح=a��حOF1ح=c�����BF1O=�ȣ���tan��=$\frac{c}{a}$=e��
�⣺��ͼ��ʾ��حBF1ح=a��حOF1ح=c�����BF1O=�ȣ���tan��=$\frac{c}{a}$=e��
���У�����Բ��������0��e��$\frac{{\sqrt{2}}}{2}$ʱ����0��tan�ȣ�$\frac{{\sqrt{2}}}{2}$��
��ȡʣ�0��$\frac{��}{4}$�������F1BF2��$\frac{��}{2}$��
����PF1F2Ϊֱ��������ʱ��ֻ���ǡ�PF1F2�͡�PF2F1Ϊֱ��ʱ������
����������ֱ�������Σ�ֻ���ĸ���
���У�����Բ��������e=$\frac{{\sqrt{2}}}{2}$ʱ����tan��=$\frac{{\sqrt{2}}}{2}$��
���=$\frac{��}{4}$����ʱ��F1BF2=$\frac{��}{2}$����ʱ��Ӧ��ֱ�������ι���������
���У�����Բ��������$\frac{{\sqrt{2}}}{2}$��e��1ʱ����tan�ȣ�$\frac{{\sqrt{2}}}{2}$����ȡʣ�$\frac{��}{4}$��$\frac{��}{2}$����
��0����F1BF2��$\frac{��}{2}$����ʱ��Ӧ��ֱ�������ι��а˸���
��ѡD��
���� ����Ҫ��������Բ�ļ����������⣬���н�����漰��Բ�ı����̼���ļ������ʣ���Բ�������ʵ�֪ʶ����ۺϿ��飬���ؿ�����ѧ����������ͽ��������������Լ����ν��˼���Ӧ�ã������е��⣮

| A�� | 2sin3 | B�� | -2sin3 | C�� | 2cos3 | D�� | -2cos3 |
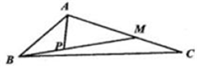 ��ͼ����֪��ABC�У���M���߶�AC�ϣ���P���߶�BM�ϣ�������$\frac{AM}{MC}$=$\frac{MP}{PB}$=2����|${\overrightarrow{AB}}$|=2��|${\overrightarrow{AC}}$|=3����BAC=120�㣬��$\overrightarrow{AP}$•$\overrightarrow{BC}$��ֵΪ-2��
��ͼ����֪��ABC�У���M���߶�AC�ϣ���P���߶�BM�ϣ�������$\frac{AM}{MC}$=$\frac{MP}{PB}$=2����|${\overrightarrow{AB}}$|=2��|${\overrightarrow{AC}}$|=3����BAC=120�㣬��$\overrightarrow{AP}$•$\overrightarrow{BC}$��ֵΪ-2��