题目内容
5.设f(x)为可导函数且满足$\underset{lim}{△x→0}$$\frac{f(1+2△x)-f(1-△x)}{△x}$=3,则函数y=f(x)图象上在点(1,f(1)处的切线的倾斜角为$\frac{π}{4}$.分析 由导数的定义,运用变形,可得在点(1,f(1)处的切线的斜率,由斜率公式,可得倾斜角.
解答 解:f(x)为可导函数且满足$\underset{lim}{△x→0}$$\frac{f(1+2△x)-f(1-△x)}{△x}$=3,
可得3$\underset{lim}{△x→0}$$\frac{f(1+2△x)-f(1-△x)}{3△x}$=3f′(1)=3,
即有f′(1)=1,
函数y=f(x)图象上在点(1,f(1)处的切线的斜率为k=1,
即tanα=1,由0≤α<π,
可得倾斜角为$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查导数的定义和几何意义,考查特殊角的正切值,考查运算能力,属于基础题.

练习册系列答案
相关题目
15.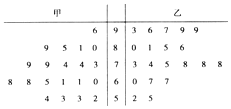 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总 计 | |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
13.某地区2012年至2016年农村居民家庭人均纯收入y(单位:千元)的数据如表:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2012年至2016年该地区农村居民家庭人均纯收入的变化情况,并预测该地区农村居民家庭人均纯收入在哪一年约为10.8千元.
附:回归直线的斜率和截距的最小二乘估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})2}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 5 | 6 | 7 | 8 | 10 |
(2)利用(1)中的回归方程,分析2012年至2016年该地区农村居民家庭人均纯收入的变化情况,并预测该地区农村居民家庭人均纯收入在哪一年约为10.8千元.
附:回归直线的斜率和截距的最小二乘估计公式分别为$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({t}_{i}-\overline{t})2}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$.
17.若$sinθ=\frac{3}{5}$,且θ是第二象限角,则cosθ=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
15.下列函数中最小正周期为π且为偶函数的是( )
| A. | $y=cos(2x-\frac{π}{2})$ | B. | $y=sin(2x+\frac{π}{2})$ | C. | $y=sin(x+\frac{π}{2})$ | D. | $y=cos(x-\frac{π}{2})$ |