题目内容
已知暗箱中开始有3个红球,2个白球(所有的球除颜色外其它均相同).现每次从暗箱中取出一个球后,再将此球以及与它同色的5个球(共6个球)一起放回箱中.
(Ⅰ)求第二次取出红球的概率;
(Ⅱ)求第三次取出白球的概率;
(Ⅲ)设取出白球得5分,取出红球得8分,求连续取球3次得分的分布列和数学期望.
(Ⅰ)求第二次取出红球的概率;
(Ⅱ)求第三次取出白球的概率;
(Ⅲ)设取出白球得5分,取出红球得8分,求连续取球3次得分的分布列和数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)设第n次取出白球、红球的概率分别为Pn,Qn,利用互斥事件加法公式能求出第二次取出红球的概率.
(Ⅱ)三次取的过程共有以下情况:白白白、白红白、红白白、红红白,由此能求出第三次取出白球的概率.
(Ⅲ)连续取球三次,得分的情况共有8种:5+5+5,8+5+5,5+8+5,5+5+8,8+8+5,8+5+8,5+8+8,8+8+8,分别求出X=15,18,21,24的概率,由此能求出连续取球3次得分的分布列和数学期望.
(Ⅱ)三次取的过程共有以下情况:白白白、白红白、红白白、红红白,由此能求出第三次取出白球的概率.
(Ⅲ)连续取球三次,得分的情况共有8种:5+5+5,8+5+5,5+8+5,5+5+8,8+8+5,8+5+8,5+8+8,8+8+8,分别求出X=15,18,21,24的概率,由此能求出连续取球3次得分的分布列和数学期望.
解答:
解:(Ⅰ)设第n次取出白球、红球的概率分别为Pn,Qn,
第二次取出红球的概率Q2=
×
+
×
=
.
(Ⅱ)三次取的过程共有以下情况:白白白、白红白、红白白、红红白,
∴第三次取出白球的概率是:
P3=
×
×
+
×
×
+
×
×
+
×
×
=
.
(Ⅲ)连续取球三次,得分的情况共有8种:
5+5+5,8+5+5,5+8+5,5+5+8,8+8+5,8+5+8,5+8+8,8+8+8,
P(X=15)=
×
×
=
,
P(X=18)=
×
×
+
×
×
+
×
×
,
P(X=21)=
×
×
+
×
×
+
×
×
=
,
P(X=24)=
×
×
=
,
∴X的分布列为:
EX=15×
+18×
+21×
+24×
=
.
第二次取出红球的概率Q2=
| 2 |
| 5 |
| 3 |
| 3+5 |
| 3 |
| 5 |
| 3+5 |
| 5+5 |
| 3 |
| 5 |
(Ⅱ)三次取的过程共有以下情况:白白白、白红白、红白白、红红白,
∴第三次取出白球的概率是:
P3=
| 2 |
| 5 |
| 2+5 |
| 5+5 |
| 2+5+5 |
| 5+5+5 |
| 2 |
| 5 |
| 3 |
| 3+5 |
| 2+5 |
| 5+5+5 |
| 3 |
| 5 |
| 2 |
| 5+5 |
| 2+5 |
| 5+5+5 |
| 3 |
| 5 |
| 3+5 |
| 5+5 |
| 2 |
| 5+5+5 |
| 2 |
| 5 |
(Ⅲ)连续取球三次,得分的情况共有8种:
5+5+5,8+5+5,5+8+5,5+5+8,8+8+5,8+5+8,5+8+8,8+8+8,
P(X=15)=
| 2 |
| 5 |
| 2+5 |
| 5+5 |
| 2+5+5 |
| 5+5+5 |
| 28 |
| 125 |
P(X=18)=
| 2 |
| 5 |
| 3 |
| 5+5 |
| 2+5 |
| 5+5+5 |
| 2 |
| 5 |
| 2+5 |
| 5+5 |
| 3 |
| 5+5+5 |
| 3 |
| 5 |
| 2 |
| 5+5 |
| 2+5 |
| 5+5+5 |
| 21 |
| 125 |
P(X=21)=
| 3 |
| 5 |
| 3+5 |
| 5+5 |
| 2 |
| 5+5+5 |
| 2 |
| 5 |
| 3 |
| 5+5 |
| 3+5 |
| 5+5+5 |
| 3 |
| 5 |
| 2 |
| 5+5 |
| 3+5 |
| 5+5+5 |
| 24 |
| 125 |
P(X=24)=
| 3 |
| 5 |
| 3+5 |
| 5+5 |
| 3+5+5 |
| 5+5+5 |
| 52 |
| 125 |
∴X的分布列为:
| X | 15 | 18 | 21 | 24 | ||||||||
| P |
|
|
|
|
| 28 |
| 125 |
| 21 |
| 125 |
| 24 |
| 125 |
| 52 |
| 125 |
| 102 |
| 5 |
点评:本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,是中档题.

练习册系列答案
相关题目
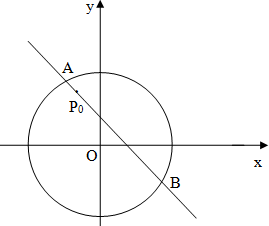 如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.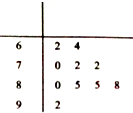 为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.
为了保护生态和环境,某市不再完全以GDP考核辖区内各县政府的政绩,广大群众的幸福指数成为考核县政府政绩的又一个重要指标,从而成立了市政府幸福办公室,其主要工作是随机抽查群众的幸福指数,为市政府提供最基础的原始数据.该办公室某工作人员在一次随机抽查了10名A县群众后,绘制了如图的茎叶图.