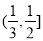题目内容
10.直线y=1分别与函数f(x)=log2(x+2),g(x)=logax的图象交于A,B两点,且AB=2.(1)求a的值;
(2)解关于x的方程,f(x)+g(x)=3.
分析 (1)令f(x)=1解出A点坐标,利用AB=2得出B点坐标,把B点坐标代入g(x)解出a;
(2)利用对数的运算性质去掉对数符号列出方程解出x,结合函数的定义域得出x的值.
解答 解:(1)解log2(x+2)=1得x=0,∴A(0,1),
∵AB=2,∴B(2,1).
把B(2,1)代入g(x)得loga2=1,∴a=2.
(2)∵f(x)+g(x)=3,
∴log2(x+2)+log2x=log2[x(x+2)]=3,
∴x(x+2)=8,解得x=-4或x=2.
由函数有意义得$\left\{\begin{array}{l}{x>0}\\{x+2>0}\end{array}\right.$,解得x>0.
∴方程f(x)+g(x)=3的解为x=2.
点评 本题考查了对数函数的图象与性质,对数方程的解法,属于基础题.

练习册系列答案
相关题目
5.已知双曲线$\frac{x^2}{9}-\frac{y^2}{4}=1$,则该双曲线的渐近线方程为( )
| A. | 9x±4y=0 | B. | 4x±9y=0 | C. | 3x±2y=0 | D. | 2x±3y=0 |
2.设M是△ABC所在平面内一点,$\overrightarrow{AC}+\overrightarrow{AB}=2\overrightarrow{AM}$则( )
| A. | $\overrightarrow{MC}+\overrightarrow{MB}=\overrightarrow 0$ | B. | $\overrightarrow{MC}+\overrightarrow{AB}=\overrightarrow 0$ | C. | $\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow 0$ | D. | $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow 0$ |
19.函数f(x)=2|x|的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
20.若x,y满足约束条件$\left\{\begin{array}{l}{x-1≥0}\\{x≤y}\\{x+y≤4}\end{array}\right.$,则$\frac{1}{x}$+$\frac{2}{y}$的最大值为( )
| A. | $\frac{5}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
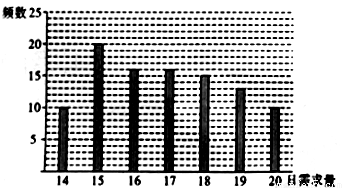
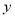 (单位:元)关于当天需求量
(单位:元)关于当天需求量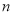 (单位:个,
(单位:个,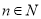 )的函数解析式;
)的函数解析式;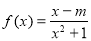 是奇函数,
是奇函数, 是偶函数.
是偶函数.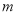 ,
,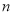 的值;
的值;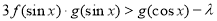 对任意
对任意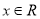 恒成立,求实数
恒成立,求实数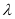 的取值范围.
的取值范围.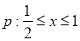 ,命题
,命题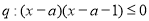 ,若
,若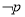 是
是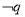 的必要不充分条件,则实数
的必要不充分条件,则实数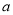 的取值范围是( )
的取值范围是( )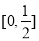 B.
B.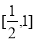
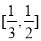 D.
D.