题目内容
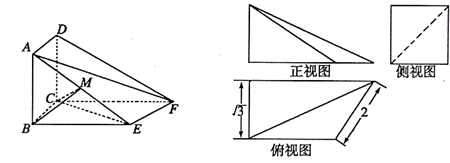
如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点. (1)求证:VD∥平面EAC;
(2)求二面角A—VB—D的余弦值.
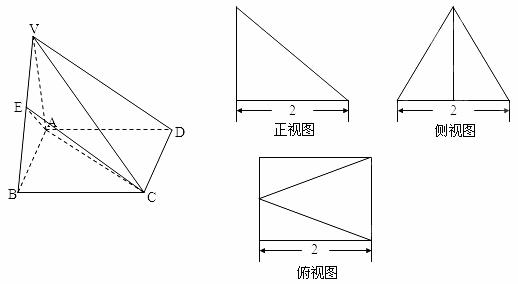
解:(1)由正视图可得:平面VAB⊥平面ABCD,连接BD交AC于O 点,连EO,由已知可得BO=OD,VE=EB
∴ VD∥EO ---------------------------------------------4
又VD![]() 平面EAC,EO
平面EAC,EO![]() 平面EAC
平面EAC
∴ VD∥平面EAC ---------------------------------------------------6
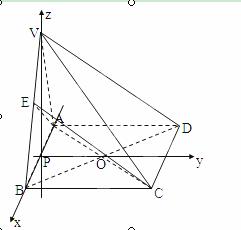
(2)设AB的中点为P,则由题意可知VP⊥平面ABCD,
建立如图所示坐标系
设![]() =(x,y,z)是平面VBD法向量,
=(x,y,z)是平面VBD法向量,
![]() =(-2,2,0)
=(-2,2,0) ![]()
![]() --------------------------8
--------------------------8
由![]() ,
,![]()
∴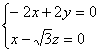
![]() -------------------------10
-------------------------10
∴二面角A—VB—D的余弦值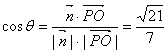 --
--

练习册系列答案
相关题目
 18、
18、 如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点.求证:VD∥平面EAC.
如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点.求证:VD∥平面EAC. (1)在正方体ABCD-A1B1C1D1中,F为AA1的中点.求证:A1C∥平面FBD
(1)在正方体ABCD-A1B1C1D1中,F为AA1的中点.求证:A1C∥平面FBD 如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点.
如图所示的多面体,它的正视图为直角三角形,侧视图为正三角形,俯视图为正方形(尺寸如图所示),E为VB的中点.