Question

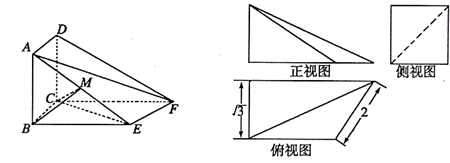
如图所示的多面体，它的正视图为直角三角形，侧视图为正三角形，俯视图为正方形（尺寸如图所示），E为VB的中点．
（1）求证：VD∥平面EAC；
（2）求二面角A-VB-D的余弦值．

Answer 1

分析：（1）欲证VD∥平面EAC，根据直线与平面平行的判定定理可知只需证VD与平面EAC内一直线平行即可，而连接BD交AC于O点，连接EO，由已知易得VD∥EO，VD?平面EAC，EO?平面EAC，满足定理条件；
（2）设AB的中点为P，则VP⊥平面ABCD，建立坐标系，利用向量的夹角公式，可求二面角A-VB-D的余弦值．

解答：（1）证明：由正视图可知：平面VAB⊥平面ABCD
连接BD交AC于O点，连接EO，由已知得BO=OD，VE=EB
∴VD∥EO
又VD?平面EAC，EO?平面EAC
∴VD∥平面EAC；
（2）设AB的中点为P，则VP⊥平面ABCD，建立如图所示的坐标系，
则

PO

=（0，1，0）
设平面VBD的法向量为

n

=(x，y，z)
∵

BD

=(-2，2，0)，

VB

=(1，0，-

3

)
∴由

n ⊥ BD n ⊥ VB

，可得

-2x+2y=0 x- 3 z=0

，∴可取

n

=（

3

，

3

，1）
∴二面角A-VB-D的余弦值cosθ=

n • PO

| n || PO |

=

21

7

点评：本题考查三视图，考查了直线与平面平行的判定，考查面面角，考查学生分析解决问题的能力，属于中档题．