题目内容
6.过点(0,1)且与双曲线x2-y2=1只有一个公共点的直线有4条.分析 由当直线与渐近线不平行时,设直线为y=kx+1,代入双曲线方程,由△=0,即可求得k=±$\sqrt{2}$,求得k的值,求得直线方程,当直线与渐近线方程平行时,直线恒过点(0,1)且渐近线平行的直线与双曲线有一个交点,成立,故过点(0,1)与双曲线x2-y2=1有且只有一个公共点的直线有4条.
解答 解:设过点(0,1)与双曲线x2-y2=1有且只有一个公共点的直线为y=kx+1.
根据题意:$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}-{y}^{2}=1}\end{array}\right.$,
消去y,整理得(1-k2)x2-2kx-2=0,
∵△=0,
∴k=±$\sqrt{2}$.
由双曲线x2-y2=1为等轴双曲线,渐近线方程为:y=±x,
由直线恒过点(0,1)且渐近线平行的直线与双曲线有一个交点,
∴当直线方程与渐近线平行时也成立.即直线方程为y±x-1=0,
故过点(0,1)与双曲线x2-y2=1有且只有一个公共点的直线有4条.
故答案为:4.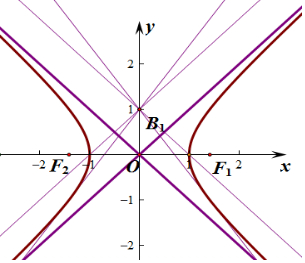
点评 本题主要考查直线与双曲线的位置关系,考查等轴双曲线的渐近线方程,考查数形结合思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在△ABC中,已知2asinA+csinC=bsinB,则∠B为( )
| A. | 钝角 | B. | 锐角 | C. | 直角 | D. | 不能 |
11.给出关于复数z=$\frac{2}{1+i}$的四个命题:p1:|z|=2;p2:z2=2i:p3:$\overline z=1+i$:p4.z的虚部为-1.下列命题中为真命题的是( )
| A. | p1∧p2 | B. | p1∨p2 | C. | (?P3)∧p4 | D. | (?p3)∨p4 |
16.已知集合A={1,2,3},B={-2,-1,0,1,2},则A∩B=( )
| A. | {1,2,3} | B. | {-2,-1,0,1,2} | C. | {1,2} | D. | {-2,-1} |
 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=