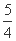题目内容
已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则Sn等于( )
(A)2n-1 (B)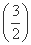 n-1 (C)
n-1 (C)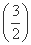 n-1 (D)
n-1 (D)
B解析:法一 由Sn=2an+1=2(Sn+1-Sn)可知,
3Sn=2Sn+1,即Sn+1= Sn,
Sn,
∴数列{Sn}是首项为S1=1,公比为 的等比数列,
的等比数列,
∴Sn=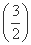 n-1.故选B.
n-1.故选B.
法二 由Sn=2an+1 ①可知a2= S1=
S1= ,
,
当n≥2时,Sn-1=2an, ②
∴①-②并化简得an+1= an(n≥2),
an(n≥2),
即{an}从第二项起是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
∴Sn=a1+ =1+
=1+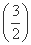 n-1-1=
n-1-1=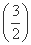 n-1(n≥2),当n=1时,满足上式.
n-1(n≥2),当n=1时,满足上式.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
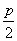 ;若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.
;若拋物线C:y2=2px(p>0)上的点到直线l1和直线l2的距离之和的最小值为2.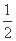 ,a4=4,则公比q= ;a1+a2+…+an= .
,a4=4,则公比q= ;a1+a2+…+an= . 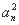 =
=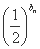 ,设cn=
,设cn=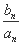 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.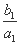 +
+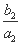 +…+
+…+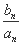 =1-
=1-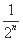 ,n∈N* ,求{bn}的前n项和Tn.
,n∈N* ,求{bn}的前n项和Tn. 的值是( )
的值是( ) (B)
(B) (C)
(C) (D)
(D)
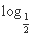 a)≤2f(1),则a的取值范围是( )
a)≤2f(1),则a的取值范围是( )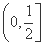 (C)
(C)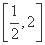 (D)(0,2]
(D)(0,2] 是定义在区间
是定义在区间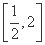 上的“兄弟函数”,那么函数f(x)在区间
上的“兄弟函数”,那么函数f(x)在区间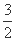 (B)2 (C)4 (D)
(B)2 (C)4 (D)