题目内容

我市某旅行社拟组团参加衡山文化一日游，预测每天游客人数在50至130 人之间，游客人数x（人）与游客的消费总额y（元）之间近似地满足关系：y=-x2+240x-10000．那么游客的人均消费额最高为
 
元．
考点：二次函数的性质
专题：函数的性质及应用
分析：利用游客的消费总额y（元）除以人数可求出游客的人均消费额，再利用基本不等式即可求出最高消费额．
解答： 解：游客的人均消费额为
y
x
=
-x2+240x-10000
x
=-（x+
10000
x
）+240≤-2
x•
10000
x
+240=40
当且仅当x=100时取等号
故答案为：40．
点评：本题以二次函数为载体，考查解不等式，考查函数模型的构建，考查基本不等式的运用，只要认真审题，解答并不难．
练习册系列答案
相关题目
指出三段论“自然数中没有最大的数字（大前提），9是最大的数字（小前提），所以9不是最大的数（结论）”中的错误是
 
．
过抛物线y2=2px（p＞0）的焦点的直线x-my+m=0与抛物线交于A、B两点，且△OAB（O为坐标原点）的面积为2
2
，则m6+m4等于（　　）
A、4B、2C、6D、8
已知简谐振动f（x）=Asin（ωx+φ）（|φ|＜
π
2
）的振幅为
3
2
，图象上相邻最高点与最低点之间的距离为5，且过点(0，
3
4
)，则该简谐振动的频率与初相分别为（　　）
A、
1
6
，
π
6
B、
1
8
，
π
6
C、
π
4
，
π
6
D、
1
6
，
π
3
已知sinα=
1
2
，α∈(0，
π
2
)．
（1）求cosα的值；
（2）求sin2α+cos2α．
已知函数f（x）=m（x+
1
x
）的图象与函数h（x）=
1
4
（x+
1
x
）+2的图象关于点A（0，1）对称．
（1）求m的值；
（2）若g（x）=f（x）+
a
4x
在区间（0，2]上为减函数，求实数a的取值范围．
准线方程为x=1的抛物线的标准方程是
 
．
P，Q是两个非空集合，定义P@Q={（a，b）|a∈P，b∈Q}，若P={2，3，4}，Q={4，5，6}，则P@Q中元素的个数（　　）
A、3个B、4C、9D、12
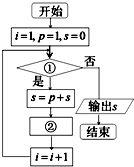给出15个数：1，2，4，7，11，…，要计算这15个数的和，现给出解决该问题的程序框图（如图所示），那么框图中判断框①处和执行框②处应分别填入（　　）
A、i≤16？；p=p+i-1
B、i≤14？；p=p+i+1
C、i≤15？；p=p+i+1
D、i≤15？；p=p+i

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网