题目内容
7．已知关于x的方程x2-（m+2）x-m+1=0有两个不等实根，则m的取值范围是（-∞，-8）∪（0，+∞）（用区间表示）．分析 若关于x的方程x2-（m+2）x-m+1=0有两个不等实根，则△=（m+2）2-4（-m+1）＞0，解得m的取值范围．
解答 解：关于x的方程x2-（m+2）x-m+1=0有两个不等实根，
则△=（m+2）2-4（-m+1）＞0，
解得：m∈（-∞，-8）∪（0，+∞），
故答案为：（-∞，-8）∪（0，+∞）
点评 本题考查的知识点是二次函数的图象和性质，熟练掌握二次函数的图象和性质，是解答的关键．
练习册系列答案
相关题目
17．命题：“?x＞0，x2-x≥0”的否定形式是（ ）
| A． | ?x≤0，x2-x＞0 | B． | ?x＞0，x2-x≤0 | C． | ?x≤0，x2-x＞0 | D． | ?x＞0，x2-x＜0 |
12．计算sin75°cos15°-cos75°sin15°的值等于（ ）
| A． | 0 | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
19．f（x）=Asin（ωx+ωπ）（A＞0，ω＞0）在$[{-\frac{3π}{2}，-\frac{3π}{4}}]$上单调，则ω的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | 1 | D． | $\frac{4}{3}$ |
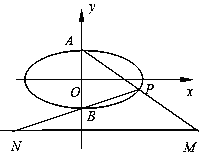如图，已知椭圆$C：\frac{x^2}{4}+{y^2}=1$的上、下顶点分别为A，B，点P在椭圆上，且异于点A，B，直线AP，BP与直线l：y=-2分别交于点M，N，