题目内容
9.在长方体OABC-O1A1B1C1中,OA=2,AB=3,AA1=2,E是BC的中点,求直线AO1与B1E所成的角的余弦值.分析 以O为原点,OA为x轴,OC为y轴,OO1为z轴,建立空间直角坐标系,利用向量法能求出直线AO1与B1E所成的角的余弦值.
解答 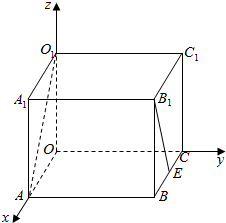 解:以O为原点,OA为x轴,OC为y轴,OO1为z轴,建立空间直角坐标系,
解:以O为原点,OA为x轴,OC为y轴,OO1为z轴,建立空间直角坐标系,
A(2,0,0),O1(0,0,2),B1(2,3,2),E(1,3,0),
$\overrightarrow{A{O}_{1}}$=(-2,0,2),$\overrightarrow{{B}_{1}E}$=(-1,0,-2),
设直线AO1与B1E所成的角为θ,
则cosθ=$\frac{|\overrightarrow{A{O}_{1}}•\overrightarrow{{B}_{1}E}|}{|\overrightarrow{A{O}_{1}}|•|\overrightarrow{{B}_{1}E}|}$=$\frac{|2+0-4|}{\sqrt{8}•\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
∴直线AO1与B1E所成的角的余弦值为:$\frac{\sqrt{10}}{10}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.已知命题p:?x0∈R,3${\;}^{{x}_{0}}$≤0;命题q:f(x)=lnx在区间(0,+∞)上是增函数,下列是真命题的是( )
| A. | p∧¬q | B. | ¬p∧¬q | C. | ¬p∧q | D. | p∧q |
4.若实数x,y满足不等式组$\left\{\begin{array}{l}{2x+y≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,则$\frac{y+1}{2x+2}$的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{5}{2}$] | B. | [$\frac{1}{3}$,5] | C. | [$\frac{2}{3}$,10] | D. | [-$\frac{1}{3}$,5] |
14.已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点在圆x2+y2=4上,过椭圆的左顶点倾斜角为$\frac{π}{3}$的直线与圆x2+y2=4相切,则椭圆的离心率( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
 如图,空间四边形ABCD中,每条边的长度和两条对角线的长度都等于1,M、N分别是AB、AD的中点,计算$\overrightarrow{MN}$•$\overrightarrow{DC}$.
如图,空间四边形ABCD中,每条边的长度和两条对角线的长度都等于1,M、N分别是AB、AD的中点,计算$\overrightarrow{MN}$•$\overrightarrow{DC}$.