题目内容

锐角三角形ABC中，a，b，c分别为角A，B，C所对的边．若2asinB=
3
b，b+c=5，bc=6，则a=
 
．
考点：正弦定理,余弦定理
专题：解三角形
分析：先求出b、c，再根据2asinB=
3
b，利用正弦定理可得sinA的值，可得cosA的值，再由余弦定理求得a的值．
解答： 解：锐角三角形ABC中，∵b+c=5，bc=6，∴
b=2
c=3
，或
b=3
c=2
．
再根据2asinB=
3
b，利用正弦定理可得2sinAsinB=
3
sinB，∴sinA=
3
2
，cosA=
1
2
．
再由余弦定理可得 a2=b2+c2-2bc•cosA=4+9-12×
1
2
=7，
∴a=
7
，
故答案为：
7
．
点评：本题主要考查正弦定理、余弦定理的应用，属于中档题．
练习册系列答案
相关题目
已知a，b∈R+，且满足log4(2a+b)=log2
ab
，则8a+b的最小值为
 
．
若a、b、c为实数，且a+b+c=1，则a2+b2+c2的最小值为
 
．
函数f（x）=x2+4x在[1，3]上的最小值是
 
．
关于x的不等式|x+1|-|x-3|≤a-
5
a
的解集不为空集，则实数a的取值范围是
 
．
已知双曲线C：
x2
a2
-
y2
b2
=1与椭圆
x2
9
+
y2
4
=1有相同的焦点，且双曲线C的渐近线方程为y=±2x，则双曲线C的方程为
 
．
复数
5i
1+2i
（i为虚数单位）的虚部是
 
．
函数f（x）=2在x=1处的导数是
 
．
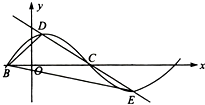已知函数f（x）=sin（2πx+φ）的部分图象如图所示，点B，C是该图象与x轴的交点，过点C的直线与该图象交于D，E两点，则（
BD
+
BE
）•
BC
的值为（　　）
A、
1
4
B、
1
2
C、1
D、2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网