题目内容
已知过点M(-3,0)的直线l被圆x2+(y+2)2=25所截得的弦长为8,那么直线l的方程为________.
x=-3或5x-12y+15=0
[解析] 因为直线被圆截得的弦长为8,所以圆心到直线的距离d=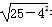 =3.当直线斜率不存在时,恰好符合,此时直线l的方程为x=-3;当直线斜率存在时,设直线l的方程为y=k(x+3),即kx-y+3k=0,所以圆心(0,-2)到直线kx-y+3k=0的距离d=
=3.当直线斜率不存在时,恰好符合,此时直线l的方程为x=-3;当直线斜率存在时,设直线l的方程为y=k(x+3),即kx-y+3k=0,所以圆心(0,-2)到直线kx-y+3k=0的距离d=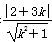 =3,解得k=
=3,解得k= ,所以直线l的方程为y=
,所以直线l的方程为y= (x+3),即5x-12y+15=0.
(x+3),即5x-12y+15=0.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,AF=1,M在EF上且AM∥平面BDE,则点M的坐标为( )
,AF=1,M在EF上且AM∥平面BDE,则点M的坐标为( )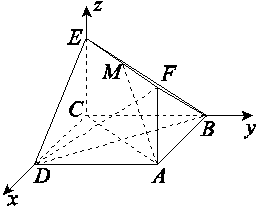
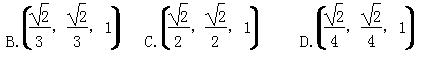
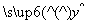 =1.23x+0.08;
=1.23x+0.08;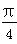 ;
;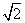 -4 B.
-4 B.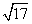 -1 C.6-2
-1 C.6-2 图象上任意一点,点Q(2a,a-3)(a∈R),则|PQ|的最小值为( )
图象上任意一点,点Q(2a,a-3)(a∈R),则|PQ|的最小值为( )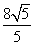 -2 B.
-2 B.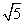 C.
C.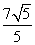 -2
-2
 恒成立,则
恒成立,则 的取值范围是 ( )
的取值范围是 ( ) B.
B. C.
C. 或
或 D.
D. 或
或
 在区间
在区间 上递减,则实数a的取值范围是__________.
上递减,则实数a的取值范围是__________.