题目内容
1.已知函数f(x)=$\frac{a}{x}$+lnx-1.(1)当a=2时,求f(x)在(1,f(1))处的切线方程;
(2)若a>0,且对x∈(0,+∞)时,f(x)>0恒成立,求实数a的取值范围.
分析 (1)求出函数的导数,计算f(1),f′(1),从而求出切线方程即可;
(2)分离参数,得到a>x(1-lnx)对x∈(0,+∞)恒成立,设g(x)=x(1-lnx),根据函数的单调性求出g(x)的最大值,从而求出a的范围即可.
解答 解:(1)a=2时,$f(x)=\frac{2}{x}+lnx-1$,
所以$f'(x)=-\frac{2}{x^2}+\frac{1}{x}$,则f'(1)=-1,
又f(1)=1,所以切线方程为y-1=-(x-1),即x+y-2=0.
(2)因为a>0,且对x∈(0,2e]时,f(x)>0恒成立,
即$\frac{a}{x}+lnx-1>0$对x∈(0,+∞)恒成立,
所以a>x(1-lnx)对x∈(0,+∞)恒成立.
设g(x)=x(1-lnx)=x-xlnx,x∈(0,+∞),
则g'(x)=1-lnx-1=-lnx,
当0<x<1时,g'(x)>0,g(x)为增函数;
当x>1时,g'(x)<0,g(x)为减函数;
所以g(x)max=g(1)=1-ln1=1,
则实数a的取值范围是(1,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及切线方程问题,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.下列命题中,正确的命题是( )
| A. | 平行于同一直线的两个平面平行 | |
| B. | 共点的三条直线只能确定一个平面 | |
| C. | 若一个平面中有无数条直线与另一个平面平行,则这两个平面平行 | |
| D. | 存在两条异面直线同时平行于同一个平面 |
9.抛物线y2=2x的焦点为F,点P在抛物线上,点O为坐标系原点,若|PF|=3,则|PO|等于( )
| A. | $\frac{3\sqrt{5}}{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{5\sqrt{5}}{2}$ | D. | 4$\sqrt{2}$ |
16. 某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h)可以把这一批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700],由于工作不慎将部分数据丢失,现有以下部分图表:
某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h)可以把这一批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700],由于工作不慎将部分数据丢失,现有以下部分图表:
(1)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(2)求图中阴影部分的面积.
 某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h)可以把这一批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700],由于工作不慎将部分数据丢失,现有以下部分图表:
某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h)可以把这一批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700],由于工作不慎将部分数据丢失,现有以下部分图表:| 分组 | [100,200] | (200,300] | (300,400] | (400,500] | (500,600] | (600,700] |
| 频数 | B | 30 | E | F | 20 | H |
| 频率 | C | D | 0.2 | 0.4 | G | I |
(2)求图中阴影部分的面积.
5.执行如图所示的程序框图,则输出S=( )
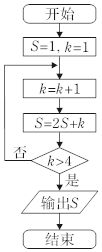

| A. | 26 | B. | 247 | C. | 120 | D. | 57 |
12.执行如图所示的程序框图,则输出的Z值为( )


| A. | 64 | B. | 6 | C. | 8 | D. | 3 |