题目内容
设a,b∈R,A={(x,y)|y=ax+b,x∈Z},B={(x,y)|y=3x2+15,x∈Z},C={(x,y)|x2+y2≤144}.是否存在a,b,使得A∩B≠∅,且(a,b)∈C?
考点:交集及其运算,元素与集合关系的判断
专题:集合
分析:根据集合的基本运算以及集合的基本关系进行判断,即可得到结论.
解答:
解:由
得3x2-ax+15-b=0有解.
则△≥0⇒a2≥12(15-b),
又a2+b2≤144⇒a2≤144-b2,
所以,144-b2≥180-12b⇒b2-12b+36≤0⇒(b-6)2≤0⇒
代入,3x2±
+9=0,得无整数解,
所以不存在.
|
则△≥0⇒a2≥12(15-b),
又a2+b2≤144⇒a2≤144-b2,
所以,144-b2≥180-12b⇒b2-12b+36≤0⇒(b-6)2≤0⇒
|
代入,3x2±
| 108 |
所以不存在.
点评:本题主要考查集合的基本运算以及集合关系的应用,利用直线和抛物线之间的关系是解决本题的关键.考查学生的运算能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
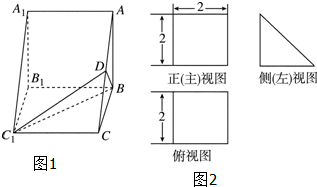 直三棱柱ABC-A1B1C1的直观图(图1)及三视图(图2)如图所示,D为AC的中点
直三棱柱ABC-A1B1C1的直观图(图1)及三视图(图2)如图所示,D为AC的中点 已知向量
已知向量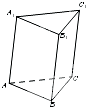 如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为
如图,在三棱柱ABC-A1B1C1中,侧棱AA1与侧面BCC1B1的距离为2,侧面BCC1B1的面积为4,此三棱柱ABC-A1B1C1的体积为