题目内容
3.已知tanφ=-$\sqrt{3}$,求sinφ,cosφ的值.分析 tanφ=-$\sqrt{3}$,可得φ=kπ+$\frac{2π}{3}$,k∈Z.代入即可得出.
解答 解:∵tanφ=-$\sqrt{3}$,
∴φ=kπ+$\frac{2π}{3}$,k∈Z.
∴当k=2n(n∈Z)为偶数时,sinφ=$sin(2nπ+\frac{2π}{3})$=$sin\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,cosφ=$\frac{sinφ}{tanφ}$=-$\frac{1}{2}$.
当k=2n+1(n∈Z)为奇数时,sinφ=$sin[(2n+1)π+\frac{2π}{3}]$=-$sin\frac{2π}{3}$=-$\frac{\sqrt{3}}{2}$,cosφ=$\frac{sinφ}{tanφ}$=$\frac{1}{2}$.
点评 本题考查了三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
13.已知两条直线:y=(a-1)x-2和3x+(a+3)y-1=0互相平行,则a等于 ( )
| A. | 0 或-2 | B. | -2 或-1 | C. | 1或-2 | D. | 0或2 |
12.时钟从3时走到4时20分,分针转了( )
| A. | 20° | B. | 480° | C. | 80° | D. | 28800° |
4.设集合U={x|x是小于9的正整数},集合A={1,2,3},集合B={3,4,5,6},则A∩(∁UB)=( )
| A. | {1,2,3} | B. | {1,2} | C. | {1,3} | D. | {2,3} |
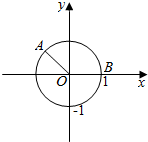 已知点A,B在单位圆上,A(-$\frac{3}{5}$,$\frac{4}{5}$),B(1,0),∠BOA=a,如图所示
已知点A,B在单位圆上,A(-$\frac{3}{5}$,$\frac{4}{5}$),B(1,0),∠BOA=a,如图所示