题目内容
【题目】在直角坐标系
中，曲线
的参数方程是
（
为参数），把曲线横坐标缩短为原来的
，纵坐标缩短为原来的一半，得到曲线
，直线
的普通方程是
，以坐标原点
为极点，
轴正半轴为极轴建立极坐标系；
（1）求直线的极坐标方程和曲线的普通方程；
（2）记射线
与交于点
，与交于点
，求
的值.
【答案】（1）直线
的极坐标方程：
；曲线
的普通方程为：
（2）
【解析】
（1）利用
化直线的直角方程为极坐标方程，先消参数得曲线
的普通方程，再根据变换得结果，（2）将直角方程化为极坐标方程，再代入
，解得
，
，即得结果.
（1）将代人直线的方程
，得：
，化简得直线的极坐标方程：
由曲线的参数方程消去参数
得曲线的普通方程为：
，
经过伸缩变换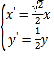
得
代入
得：
，
即
，
故曲线的普通方程为：
（2）由（1）将曲线的普通方程化为极坐标方程：
，
将
代人得
，
将代入得：
，
故
.
练习册系列答案
阅读快车系列答案
相关题目
