题目内容
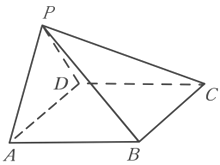
【题目】如图,在长方体![]() 中,
中,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,则下列结论正确的是( )
上的动点,则下列结论正确的是( )
A.当![]() 时,
时,![]() 三点共线
三点共线
B.当![]() 时,
时,![]()
C.当![]() 时,
时,![]() 平面
平面![]()
D.当![]() 时,
时,![]() 平面
平面![]()
【答案】ACD
【解析】
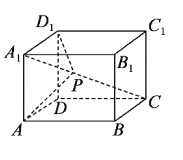
在长方体![]() 中,以点
中,以点![]() 为坐标原点,建立空间直角坐标系,得到对应点的坐标,以及
为坐标原点,建立空间直角坐标系,得到对应点的坐标,以及![]() ,
,![]() ;根据空间向量的方法,逐项判断,即可得出结果.
;根据空间向量的方法,逐项判断,即可得出结果.
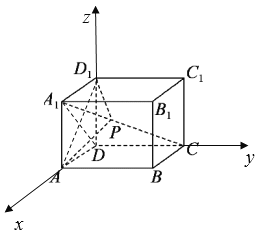
在长方体![]() 中,以点
中,以点![]() 为坐标原点,建立如图所示的空间直角坐标系,
为坐标原点,建立如图所示的空间直角坐标系,
因为![]() ,所以
,所以![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ;
;
A选项,当![]() 时,
时,![]() 为
为![]() 中点,根据长方体结构特征,
中点,根据长方体结构特征,![]() 为体对角线的中点,因此
为体对角线的中点,因此![]() 也为
也为![]() 中点,所以
中点,所以![]() 三点共线;故A正确;
三点共线;故A正确;
B选项,当![]() 时,
时,![]() ,由题意可得,
,由题意可得,![]() ,
,![]() ,所以由
,所以由![]() ,解得:
,解得:![]() ,所以
,所以![]() ,即点
,即点![]() 为靠近点
为靠近点![]() 的五等分点,所以
的五等分点,所以 ,则
,则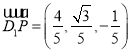 ,
,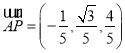 ,所以
,所以![]() ,所以
,所以![]() 与
与![]() 不垂直,故B错误;
不垂直,故B错误;
C选项,当![]() 时,则
时,则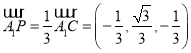 ,
,
设平面![]() 的法向量为
的法向量为![]() ,由
,由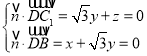 ,令
,令![]() ,可得:
,可得:![]() ,又
,又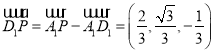 ,
,
所以![]() ,因此
,因此![]() ,所以
,所以![]() 平面
平面![]() ;
;
D选项,当![]() 时,
时,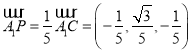 ,所以
,所以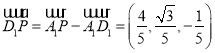 ,
,
所以![]() ,
,![]() ,因此
,因此![]() ,
,![]() ,根据线面垂直定理,可得
,根据线面垂直定理,可得![]() 平面
平面![]() .
.
故选:ACD.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目