题目内容
 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4),则
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(4,4),则| lim |
| △x→0 |
| f(3+△x)-f(3) |
| △x |
| A、1 | B、-1 | C、2 | D、-2 |
分析:先结合函数的图象的性质,求出f(x)=
,由此能够得到
=f′(3)=2.
|
| lim |
| △x→0 |
| f(3+△x)-f(3) |
| △x |
解答:解:由图象知,当0≤x≤2时,
设y=kx+b,把(0,4),(2,0)代入,得
,∴b=4,k=-2,y=-2x+4.
当2≤x≤4时,
设y=mx+n,把(4,4),(2,0)代入,得
,∴m=2,n=-4,y=2x-4.
故f(x)=
.
∴
=f′(3)=2.
故选C.
设y=kx+b,把(0,4),(2,0)代入,得
|
当2≤x≤4时,
设y=mx+n,把(4,4),(2,0)代入,得
|
故f(x)=
|
∴
| lim |
| △x→0 |
| f(3+△x)-f(3) |
| △x |
故选C.
点评:本题考查极限的性质和应用,解题时要注意分段函数和数形结合法的运用,考查计算能力.

练习册系列答案
相关题目
 4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))=
4、如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(1))= 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(2))= 如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集.
如图,函数f(x)的图象为单位圆上的两段弧,求不等式f(x)-f(-x)>x的解集. 如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(
如图,函数f(x)的图象是折线段ABC,其中A(0,4),B(2,0),C(6,4),则f(f(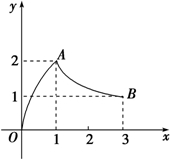 (2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(
(2012•云南模拟)如图,函数f(x)的图象是曲线OAB,其中点O,A,B的坐标分别为(0,0),(1,2),(3,1),则f(