题目内容
已知函数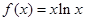 ,
,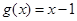 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若对任意正实数x,不等式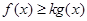 恒成立,求实数k的值;
恒成立,求实数k的值;
(Ⅲ)求证: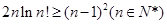 .(其中
.(其中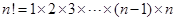 )
)
(Ⅰ)单调递减区间为 ,单调递增区间为
,单调递增区间为
(Ⅱ) (Ⅲ)利用放缩不等式可以证明,或用数学归纳法证明
(Ⅲ)利用放缩不等式可以证明,或用数学归纳法证明
解析试题分析:(Ⅰ)易知函数的定义域为 ,
, ;
;
(Ⅱ)解法一:







综上: ;
;
解法二:


由题意 ,
,

 ,
,
(Ⅲ)证法一:


 ,并累加得:
,并累加得:



证法二:数学归纳法(略)
考点:本小题主要考查用导数研究函数的单调性、极值、最值等性质,以及放缩法或数学归纳法证明不等式,考查学生的运算求解能力和推理论证能力.
点评:用导数研究函数的单调性、极值、最值等性质时,不要忘记先求函数的定义域,用放缩法证明不等式时,要注意放缩的力度要恰当,如果用数学归纳法证明,需要严格按步骤进行.

练习册系列答案
相关题目
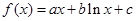 ,
,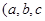 是常数)在x=e处的切线方程为
是常数)在x=e处的切线方程为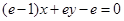 ,
, 既是函数
既是函数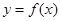 的零点,又是它的极值点.
的零点,又是它的极值点. 在区间(1,3)内不是单调函数,求实数m的取值范围;
在区间(1,3)内不是单调函数,求实数m的取值范围;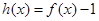 的单调递减区间,并证明:
的单调递减区间,并证明: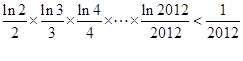
 对于任意实数
对于任意实数 满足
满足 ,当
,当 时,
时, .
. 并判断
并判断 ,集合
,集合 ,
, ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.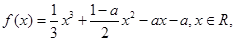 其中
其中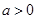 .(1)求函数
.(1)求函数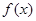 的单调区间;(2)若函数
的单调区间;(2)若函数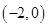 内恰有两个零点,求
内恰有两个零点,求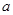 的取值范围;
的取值范围;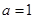 时,设函数
时,设函数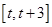 上的最大值为
上的最大值为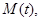 最小值为
最小值为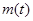 ,记
,记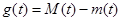 ,求函数
,求函数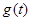 在区间
在区间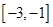 上的最小值.
上的最小值.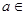 R,函数
R,函数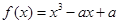 .
.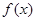 的单调区间;
的单调区间;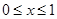 时,
时,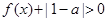 .
.
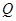 (百件)与销售价格
(百件)与销售价格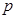 (元)的关系如下图,每月各种开支2000元.
(元)的关系如下图,每月各种开支2000元.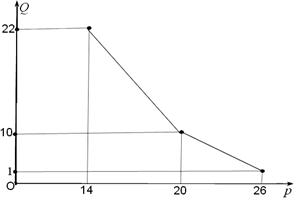
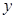 (元)与销售价格
(元)与销售价格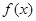
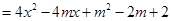 的图像与
的图像与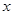 轴有两个交点
轴有两个交点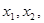 试判断函数
试判断函数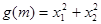 有没有最大值或最小值,并说明理由.
有没有最大值或最小值,并说明理由.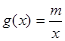 在区间
在区间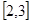 上都是减函数,求实数
上都是减函数,求实数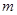 的取值范围.
的取值范围.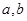 是方程
是方程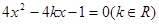 的两个不等实根,函数
的两个不等实根,函数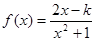 的定义域为
的定义域为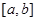 .
.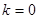 时,求函数
时,求函数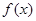 的值域;
的值域;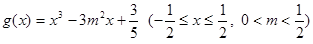 ,
, 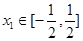 ,总存在
,总存在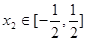 ,使得
,使得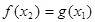 成立,
成立,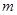 的取值范围.
的取值范围.