题目内容
如图,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
,![]() ,且
,且![]() ,O为
,O为![]() 中点.(Ⅰ)在
中点.(Ⅰ)在![]() 上确定一点
上确定一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;(Ⅱ)求二面角
,并说明理由;(Ⅱ)求二面角![]() 的大小.
的大小.


解:(Ⅰ) ![]() 为
为![]() 中点. --------------2分
中点. --------------2分
证法一:取![]() 中点
中点![]() ,连接
,连接![]() . --------------3分
. --------------3分
所以可得![]() ,所以面
,所以面![]() 面
面![]() .
.
所以![]() 平面
平面![]() .------------ 6分
.------------ 6分
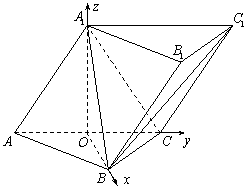 证法二:因为
证法二:因为![]() ,且O为
,且O为![]()
的中点,所以![]() .又由题意可知,
.又由题意可知,
平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,
且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
以O为原点,![]() 所在直线分别
所在直线分别
为x,y,z轴建立空间直角坐标系.…………1分
由题意可知,![]() 又
又![]()
![]()
所以得:![]()
则有:![]() . ------------2分
. ------------2分
设平面![]() 的一个法向量为
的一个法向量为![]() ,则有
,则有
![]() ,令
,令![]() ,得
,得![]()
所以![]() . ------------------4分
. ------------------4分
设![]() 即
即![]() ,得
,得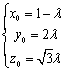
所以![]() 得
得![]() 由已知
由已知![]() 平面
平面![]() ,
,
得![]() , 即
, 即![]() 得
得![]() .
.
即存在这样的点![]() ,
,![]() 为
为![]() 的中点. ----------------6分
的中点. ----------------6分
|
![]() ,则,
,则,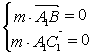
![]()
令![]() ,所以.
,所以. ![]() -----------------8分
-----------------8分
所以![]() <
<![]() ,
,![]() >=
>= ![]() =
=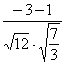 =
= ![]() .-------- 10分
.-------- 10分
由图可得二面角![]() 的大小为
的大小为![]() . -----------12分
. -----------12分

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
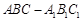 中,侧面
中,侧面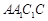
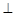 底面
底面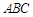 ,
,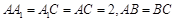 ,且
,且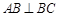 ,O为
,O为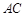 中点.
中点.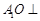 平面
平面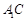 与平面
与平面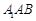 所成角的正弦值
所成角的正弦值 中,侧面
中,侧面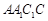
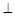 底面
底面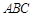 ,
,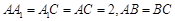 ,且
,且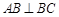 ,O为
,O为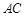 中点.
中点.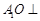 平面
平面 与平面
与平面 所成角的正弦值
所成角的正弦值
 中,侧面
中,侧面
 底面
底面 ,
, ,且
,且 ,O为
,O为 中点.
中点.
 平面
平面 与平面
与平面 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 中,侧面
中,侧面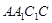
 底面
底面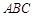 ,
,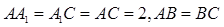 ,且
,且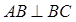 ,O为
,O为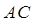 中点.
中点.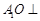 平面
平面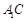 与平面
与平面 所成角的正弦值;
所成角的正弦值;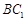 上是否存在一点
上是否存在一点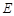 ,使得
,使得 平面
平面
 中,侧面
中,侧面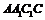
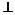 底面
底面 ,
, ,
, 且
且 ,O为
,O为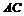 中点.
中点.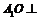 平面
平面 与平面
与平面 所成角的正弦值;
所成角的正弦值;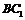 上是否存在一点
上是否存在一点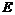 ,使得
,使得 平面
平面