题目内容
在△ABC中,点D和E分别在BC上,且 ,AD与BE交于R,证明:
,AD与BE交于R,证明: .
.
【答案】分析:由A、D、R三点共线,可得 =
= .由B、E、R三点共线,可得
.由B、E、R三点共线,可得 =
= .根据平面向量的基本定理,可构造λ和μ的方程,进而求出λ,μ值,进而根据向量减法的三角形法则,得到答案.
.根据平面向量的基本定理,可构造λ和μ的方程,进而求出λ,μ值,进而根据向量减法的三角形法则,得到答案.
解答:证明:由A、D、R三点共线,
可得 =
= .
.
由B、E、R三点共线,
可得 =
= .
.
∴
∴ …(6分)
…(6分)
∴
∴
 =
= =
= …(12分)
…(12分)
点评:本题考查的知识点是向量在几何中的应用,熟练掌握向量共线的充要条件及平面向量的基本定理是解答的关键.
 =
= .由B、E、R三点共线,可得
.由B、E、R三点共线,可得 =
= .根据平面向量的基本定理,可构造λ和μ的方程,进而求出λ,μ值,进而根据向量减法的三角形法则,得到答案.
.根据平面向量的基本定理,可构造λ和μ的方程,进而求出λ,μ值,进而根据向量减法的三角形法则,得到答案.解答:证明:由A、D、R三点共线,
可得
 =
= .
.由B、E、R三点共线,
可得
 =
= .
.∴

∴
 …(6分)
…(6分)∴

∴

 =
= =
= …(12分)
…(12分)点评:本题考查的知识点是向量在几何中的应用,熟练掌握向量共线的充要条件及平面向量的基本定理是解答的关键.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 在△ABC中,点D和E分别在BC上,且
在△ABC中,点D和E分别在BC上,且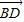 =2
=2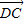 ,用
,用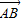 和
和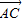 表示
表示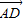 .
.