题目内容
(本小题满分12分)已知二次函数 的图像经过坐
的图像经过坐 标原
标原 点,且满足
点,且满足 ,设函数
,设函数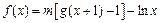 ,其中m为常数且
,其中m为常数且 。
。
(1)求函数 的解析式;
的解析式;
(2)判断函数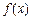 的单调性并说明理由。
的单调性并说明理由。
 的图像经过坐
的图像经过坐 标原
标原 点,且满足
点,且满足 ,设函数
,设函数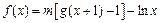 ,其中m为常数且
,其中m为常数且 。
。(1)求函数
 的解析式;
的解析式;(2)判断函数
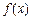 的单调性并说明理由。
的单调性并说明理由。(1)设 ,由
,由 的图象经过坐标原点得
的图象经过坐标原点得



 …………………………………………………………………
………………………………………………………………… ………5分
………5分
(2)函数


从而 [
[


 ……………………………………………………12分
……………………………………………………12分
 ,由
,由 的图象经过坐标原点得
的图象经过坐标原点得



 …………………………………………………………………
………………………………………………………………… ………5分
………5分(2)函数



从而
 [
[

 ……………………………………………………12分
……………………………………………………12分略

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 =x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式.
=x2+2x-5,x∈[t,t+1],若f(x)的最小值为h(t),写出h(t)的表达式. .
. 时,求不等式
时,求不等式 的解集;
的解集; 的解集为
的解集为 ,求
,求 的值.
的值. .
.  时,求函数f(x)
时,求函数f(x) 的最大值和最小值;
的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数
上是单调函数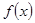 在
在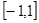 上是增函数,且
上是增函数,且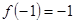 ,当
,当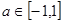 时,
时, 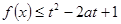 对所有的
对所有的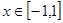 恒成立,则
恒成立,则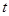 的取值范围是( )
的取值范围是( ) 或
或 或
或
 或
或 或
或
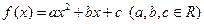 满足下列条件:
满足下列条件: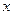 ∈R时,
∈R时,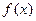 的最小值为0,且f (
的最小值为0,且f (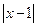 +1恒成立。
+1恒成立。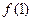 的值;
的值; 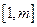 时,就有
时,就有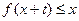 成立。
成立。 ,满足
,满足 为偶函数,且方程
为偶函数,且方程 有相等实根。
有相等实根。 的解析式;
的解析式; 上的最大值。
上的最大值。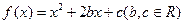 。(1)若
。(1)若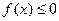 的解集
的解集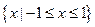 ,求实数
,求实数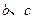 的值;(2)若
的值;(2)若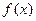 满足
满足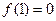 ,且关于
,且关于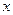 的方程
的方程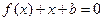 的两个实根分别在区间
的两个实根分别在区间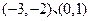 内,求实数
内,求实数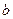 的取值范围。
的取值范围。 +c的图象的开口向下,对称轴为x=1,方程 ax2+bx+c=0的两个解一个在区间(2,3)中,则下列判断正确的是
+c的图象的开口向下,对称轴为x=1,方程 ax2+bx+c=0的两个解一个在区间(2,3)中,则下列判断正确的是