题目内容
2.函数y=sinx定义域为[a,b],值域为[-1,$\frac{\sqrt{3}}{2}$],则b-a的最大值与最小值之和等于( )| A. | 4π | B. | $\frac{7π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
分析 结合y=sinx的图象求出使值域为[-1,$\frac{\sqrt{3}}{2}$]时,定义域是[-$\frac{4π}{3}$,$\frac{π}{3}$]的子集,其中必须含-$\frac{π}{2}$.
解答 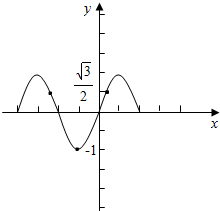 解:∵值域为[-1,$\frac{\sqrt{3}}{2}$],
解:∵值域为[-1,$\frac{\sqrt{3}}{2}$],
由y=sinx的图象,
得:b-a的最大值为:$\frac{π}{3}$-(-$\frac{4π}{3}$)=$\frac{5π}{3}$;
最小值为 $\frac{π}{3}$-(-$\frac{π}{2}$)=$\frac{5π}{6}$.
∴$\frac{5π}{3}$+$\frac{5π}{6}$=$\frac{15π}{6}$=$\frac{3π}{2}$.
故选:C.
点评 本题考查通过正弦函数的图象求定义域、值域间的关系,属于基础题.

练习册系列答案
相关题目
6.下列集合中是方程组$\left\{\begin{array}{l}{x+y=1}\\{x-y=-1}\end{array}\right.$的解集的为( )
| A. | {1,0} | B. | {0,1} | C. | {(x,y)|$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$} | D. | Φ |
4.已知集含A={(x,y)|y=f(x)},B={(x,y)|x=a,y∈R},其中a为常数,则集合A∩B的元素有( )
| A. | 0个 | B. | 1个 | C. | 至多1个 | D. | 至少1个 |
14.若$\frac{2}{1-i}$=1-ai,其中a是实数,i是虚数单位,则a=( )
| A. | 1 | B. | 2 | C. | 3 | D. | -1 |