题目内容
7.在△ABC中,a=$\sqrt{3}$,b=$\sqrt{2}$,B=45°.求角A,C和边c.分析 根据正弦定理进行求解即可.
解答 解:∵$\frac{a}{sinA}$=$\frac{b}{sinB}$,
∴sinA=$\frac{asinB}{b}$=$\frac{\sqrt{3}×\frac{\sqrt{2}}{2}}{\sqrt{2}}$=$\frac{\sqrt{3}}{2}$,
∵a>b.∴A>B,
即A=60°或120°,
若A=60°,则C=180°-60°-45°=75°,
由$\frac{a}{sinA}$=$\frac{c}{sinC}$,得c=$\frac{a}{sinA}$•sinC=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}×$sin75°=2×$\frac{\sqrt{2}}{2}$($\frac{1}{2}$+$\frac{\sqrt{3}}{2}$)=$\frac{\sqrt{2}+\sqrt{6}}{2}$.
若A=120°,则C=180°-120°-45°=15°,
由$\frac{a}{sinA}$=$\frac{c}{sinC}$,得c=$\frac{a}{sinA}$•sinC=$\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}×$sin15°=2×$\frac{\sqrt{2}}{2}$($\frac{\sqrt{3}}{2}$-$\frac{1}{2}$)=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
点评 本题主要考查解三角形的应用,利用正弦定理是解决本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
18.设p:x2-5x+a<0; q:x2-4x+3<0或2${\;}^{{x}^{2}}$<26x-8
(1)当a=6时,“p∨q”为真,求x的范围
(2)¬p是¬q的充分不必要条件时,求a的取值范围.
(1)当a=6时,“p∨q”为真,求x的范围
(2)¬p是¬q的充分不必要条件时,求a的取值范围.
15.若α为锐角且cos(α+$\frac{π}{4}$)=$\frac{3}{5}$,则cosα=( )
| A. | $\frac{\sqrt{2}}{5}$ | B. | $\frac{6\sqrt{2}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{7\sqrt{2}}{10}$ |
19.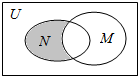 设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
 设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )
设全集U为实数集R,N={x|1<x<3},M={x|x>2},则图中阴影部分所表示的集合是( )| A. | {x|x<2} | B. | {x|-2≤x≤2} | C. | {x|-2≤x<1} | D. | {x|1<x≤2} |