题目内容
如图,已知抛物线 上横坐标为4的点到焦点的距离为5.
上横坐标为4的点到焦点的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)设直线 与抛物线C交于两点
与抛物线C交于两点 ,
, ,且
,且 (a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到
(a为正常数).过弦AB的中点M作平行于x轴的直线交抛物线C于点D,连结AD、BD得到 .
.
(i)求实数a,b,k满足的等量关系;
(ii) 的面积是否为定值?若为定值,求出此定值;若不是定值,请说明理由.
的面积是否为定值?若为定值,求出此定值;若不是定值,请说明理由.
(Ⅰ)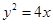 (Ⅱ)(i)
(Ⅱ)(i) (ii)为定值
(ii)为定值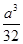
解析试题分析:(Ⅰ)依题意: ,解得
,解得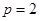 .
.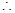 抛物线方程为
抛物线方程为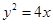 .
.
(Ⅱ)(i)由方程组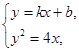 消去
消去 得:
得: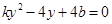 .(※)
.(※)
依题意可知: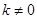 .
.
由已知得 ,
, .
.
由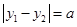 ,得
,得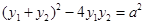 ,即
,即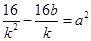 ,整理得
,整理得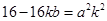 .
.
所以 .
.
(ii)由(i)知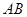 中点
中点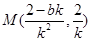 ,所以点
,所以点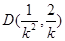 ,
,
依题意知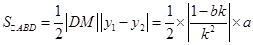 .
.
又因为方程(※)中判别式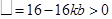 ,得
,得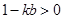 .
.
所以 ,
,
由(Ⅱ)可知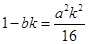 ,所以
,所以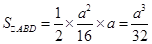 .
.
又 为常数,故
为常数,故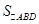 的面积为定值.
的面积为定值.
考点:本小题主要考查抛物线标准方程的求解,直线与抛物线的位置关系的判断和应用,三角形面积公式的应用,考查学生的运算求解能力.
点评:判断直线与抛物线的位置关系时,不要忘记验证判别式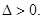

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
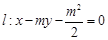 ,椭圆C:
,椭圆C: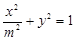 ,
, 、
、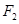 分别为椭圆C的左、右焦点.
分别为椭圆C的左、右焦点.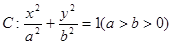 的左右焦点分别为
的左右焦点分别为 ,
, ,上顶点为
,上顶点为 ,过点
,过点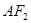 垂直的直线交
垂直的直线交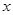 轴负半轴于
轴负半轴于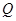 点,且
点,且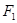 是
是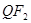 的中点.
的中点.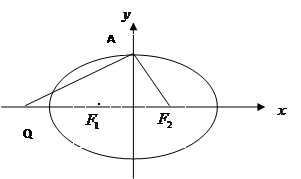
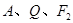 的圆恰好与直线
的圆恰好与直线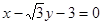 相切,求椭圆
相切,求椭圆 的方程;
的方程;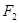 作斜率为
作斜率为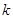 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,在
两点,在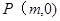 使得以
使得以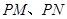 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。 的离心率为
的离心率为 ,且过点
,且过点 ,
, 为其右焦点.
为其右焦点. 的方程;
的方程;  的直线
的直线 与椭圆相交于
与椭圆相交于 、
、 两点(点
两点(点 两点之间),若
两点之间),若 与
与 的面积相等,试求直线
的面积相等,试求直线 是椭圆
是椭圆 的右顶点,若点
的右顶点,若点 在椭圆上,且满足
在椭圆上,且满足 .(其中
.(其中 为坐标原点)
为坐标原点)
 与椭圆交于两点
与椭圆交于两点 ,当
,当 时,求
时,求 面积的最大值.
面积的最大值. 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,曲线
,曲线 的内切圆半径为
的内切圆半径为 .记
.记 为以曲线
为以曲线 是过椭圆
是过椭圆 是线段
是线段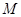 是
是 (
( 为坐标原点),当点
为坐标原点),当点 在椭圆
在椭圆 的面积的最小值.
的面积的最小值.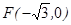 ,且过
,且过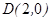 ,设点
,设点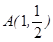 .
.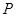 是椭圆上的动点,求线段
是椭圆上的动点,求线段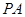 中点
中点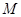 的轨迹方程。
的轨迹方程。 ,它的离心率为
,它的离心率为 ,一个焦点和抛物线
,一个焦点和抛物线 的焦点重合,过直线
的焦点重合,过直线 上一点M引椭圆
上一点M引椭圆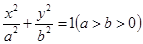 上的点
上的点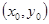 处的椭圆的切线方程是
处的椭圆的切线方程是 . 求证:直线
. 求证:直线 恒过定点
恒过定点 ;并出求定点
;并出求定点 ,使得
,使得 恒成立?(点
恒成立?(点
 的离心率为
的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,且以
两点,且以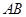 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
, 面积的最大值.
面积的最大值.