题目内容
(本小题满分10分)
已知抛物线 与直线
与直线 交于
交于 两点.
两点.
(Ⅰ)求弦 的长度;
的长度;
(Ⅱ)若点 在抛物线
在抛物线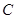 上,且
上,且 的面积为
的面积为 ,求点P的坐标.
,求点P的坐标.
(Ⅰ) 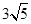 (Ⅱ) (9,6)或(4,-4)
(Ⅱ) (9,6)或(4,-4)
解析试题分析:(Ⅰ)设A(x1,y1)、B(x2,y2),
由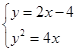 得x2-5x+4=0,Δ>0.
得x2-5x+4=0,Δ>0.
法一:又由韦达定理有x1+x2=5,x1x2=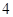 ,
,
∴|AB|=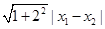 =
=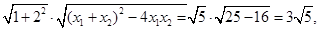
法二:解方程得:x=1或4,∴A、B两点的坐标为(1,-2)、(4,4)
∴|AB|=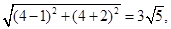
(Ⅱ)设点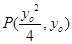 ,设点P到AB的距离为d,则
,设点P到AB的距离为d,则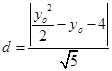 ,∴S△PAB=
,∴S△PAB=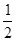 ·
·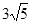 ·
·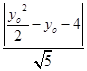 =12,
=12,
∴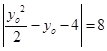 . ∴
. ∴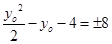 ,解得
,解得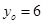 或
或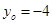
∴P点为(9,6)或(4,-4).
考点:直线与椭圆的位置关系
点评:直线与圆锥曲线相交,联立方程利用韦达定理是常用的思路

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 是椭圆
是椭圆 的右顶点,若点
的右顶点,若点 在椭圆上,且满足
在椭圆上,且满足 .(其中
.(其中 为坐标原点)
为坐标原点)
 与椭圆交于两点
与椭圆交于两点 ,当
,当 时,求
时,求 面积的最大值.
面积的最大值.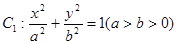 经过点
经过点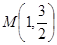 ,且其右焦点与抛物线
,且其右焦点与抛物线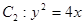 的焦点F重合.
的焦点F重合. 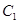 的方程;
的方程;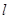 经过点
经过点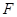 与椭圆
与椭圆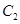 相交于C、D两点.求
相交于C、D两点.求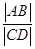 的最大值.
的最大值.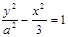 的焦点为F1,F2.离心率为2。
的焦点为F1,F2.离心率为2。 ,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。
,求线段AB中点M的轨迹方程,并说明轨迹是什么曲线。 过点
过点 ,且离心率为
,且离心率为 .
. 的方程;
的方程; 为椭圆
为椭圆 是椭圆
是椭圆 分别交直线
分别交直线 于
于 两点.
两点. 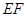 为直径的圆恒过
为直径的圆恒过 轴上的定点.
轴上的定点.
 的离心率为
的离心率为 ,且椭圆上一点与椭圆的两个焦点构成的三角形周长为
,且椭圆上一点与椭圆的两个焦点构成的三角形周长为 .
. 的方程;
的方程; 与椭圆
与椭圆 两点,且以
两点,且以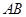 为直径的圆过椭圆的右顶点
为直径的圆过椭圆的右顶点 ,
, 面积的最大值.
面积的最大值.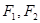 分别是椭圆的
分别是椭圆的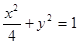 左,右焦点。
左,右焦点。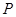 是第一象限内该椭圆上的一点,且
是第一象限内该椭圆上的一点,且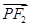 ·
·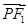 =
=
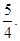 求点
求点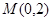 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点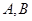 ,且
,且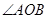 为锐角(其中O为坐标原点),求直线
为锐角(其中O为坐标原点),求直线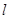 的斜率
的斜率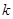 的取值范围。
的取值范围。 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2: 与
与 轴的交点为B,且经过F1,F2点.
轴的交点为B,且经过F1,F2点.
 ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求 面积的最大值.
面积的最大值. 的离心率为
的离心率为 ,焦点在
,焦点在 轴上,且长轴长为10,曲线
轴上,且长轴长为10,曲线 上的点与椭圆
上的点与椭圆