题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且cos(A-B)cosB-sin(A-B)sin(A+C)
=- .
.
(1)求sinA的值;
(2)若a=4 ,b=5,求向量
,b=5,求向量 在
在 方向上的投影.
方向上的投影.
(1)  (2)
(2)  cosB=
cosB=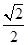
解析解:(1)由cos(A-B)cosB-sin(A-B)sin(A+C)=- ,
,
得cos(A-B)cosB-sin(A-B)sinB=- .
.
则cos(A-B+B)=- ,
,
即cosA=- .
.
又0<A<π,则sinA= .
.
(2)由正弦定理,有 =
= ,
,
所以sinB= =
=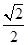 .
.
由题知a>b,则A>B,故B= .
.
根据余弦定理,有(4 )2=52+c2-2×5c×
)2=52+c2-2×5c× ,解得c=1或c=-7(负值舍去).
,解得c=1或c=-7(负值舍去).
故向量 在
在 方向上的投影为
方向上的投影为 cosB=
cosB=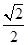 .
.

练习册系列答案
相关题目
 中,
中,
 的值;
的值; ,则
,则 、
、 、
、 为正实数,
为正实数, .
. 的三边长,且
的三边长,且 、
、 、
、 .若
.若 ,且
,且 .求
.求 .试证明长为
.试证明长为 .
.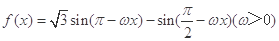 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为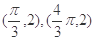 .
. 的值;
的值;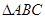 中,
中,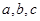 分别是角
分别是角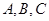 的对边,且
的对边,且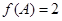 ,求
,求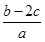 的取值范围.
的取值范围. 中,
中, ,
,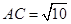 ,
,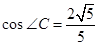 点
点 是
是 的中点, 求
的中点, 求
 的值和中线
的值和中线 的长
的长 与n=(3,sinA+
与n=(3,sinA+ cosA)共线,其中A是△ABC的内角.
cosA)共线,其中A是△ABC的内角. ,
, 的最大值为2.
的最大值为2. 在
在 上的值域;
上的值域; 外接圆半径
外接圆半径 ,
, ,角
,角 所对的边分别是
所对的边分别是 ,求
,求 的值.
的值.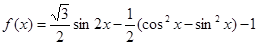
 的最小值和最小正周期;
的最小值和最小正周期; 的对边分别为a,b,c且
的对边分别为a,b,c且 =
= ,
, ,若向量
,若向量 共线,求
共线,求 的值.
的值.