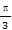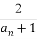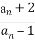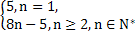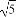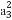题目内容
在等差数列{an}中,a1=3,其前n项和为Sn,等比数列{bn}的各项均为正数,b1=1,公比为q,且b2+S2=12,q=
.
(1)求an与bn.
(2)证明:
≤
+
+…+
<
.
(1) an=3n,bn=3n-1 (2)见解析
【解析】(1)设{an}的公差为d,
因为
所以
解得q=3或q=-4(舍),d=3.
故an=3+3(n-1)=3n,bn=3n-1.
(2)因为Sn=
,
所以
=
=
(
-
).
故
+
+…+
=[(1-
)+(-
)+(-
)+…+(-)]
=(1-).
因为n≥1,所以0<≤,于是≤1-<1,
所以≤(1-)<.
即≤++…+<.
练习册系列答案
相关题目
