题目内容
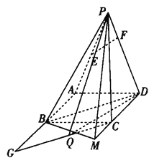
【题目】如图,在三棱锥![]() 中,
中,![]() 为等腰直角三角形,
为等腰直角三角形,![]() 为等边三角形,其中O为BC中点,且
为等边三角形,其中O为BC中点,且![]() .
.
(1)求证:平面![]() 平面PBC;
平面PBC;
(2)若![]() 且
且![]() 平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
平面EBC,其中E为AP上的点,求CE与平面ABC所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由题意可得![]() ,
,![]() ,利用线面垂直的判定定理证出
,利用线面垂直的判定定理证出![]() 平面PAO,从而得证.
平面PAO,从而得证.
(2)作PH垂直于平面ABC,垂足为H,由(1)知,点H在直线AO上,以A为原点,AC为x轴,AB为y轴,以过A点与平面ABC垂直的直线为z轴建立空间直角坐标系,求出![]() 以及平面ABC的一个法向量,利用空间向量的数量积即可求解.
以及平面ABC的一个法向量,利用空间向量的数量积即可求解.
(1) 证明:由题可知,![]() ,
,![]() ,且
,且![]() ,
,
故![]() 平面PAO,又
平面PAO,又![]() 平面PBC,因此平面
平面PBC,因此平面![]() 平面PBC.
平面PBC.
(2)作PH垂直于平面ABC,垂足为H,由(1)知,点H在直线AO上.
如图,以A为原点,AC为x轴,AB为y轴,以过A点与平面ABC垂直的直线为z轴建立空间直角坐标系,可得如下坐标:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设P点坐标为![]() ,利用
,利用![]() ,
,![]() ,可得
,可得![]() .从
.从![]() .
.
因为E为AP上的点,故存在实数![]() ,使得
,使得![]() ,点E坐标可设为
,点E坐标可设为![]() ,
,
由![]() 平面EBC知,
平面EBC知,![]() ,得
,得![]() ,
,
从而![]() ,取平面ABC的一个法向量
,取平面ABC的一个法向量![]() .
.
设CE与平面ABC所成角的为![]() ,
,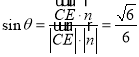 .
.
故CE与平面ABC所成角的正弦值为![]() .
.


 阅读快车系列答案
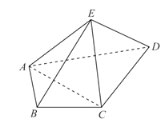
阅读快车系列答案【题目】设三棱锥![]() 的每个顶点都在球
的每个顶点都在球![]() 的球面上,
的球面上,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
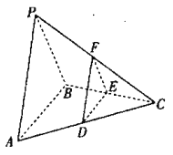
(1)确定![]() 的位置(需要说明理由),并证明:平面
的位置(需要说明理由),并证明:平面![]() 平面
平面![]() .
.
(2)与侧面![]() 平行的平面
平行的平面![]() 与棱
与棱![]() ,
,![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,
,![]() ,求四面体
,求四面体![]() 的体积的最大值.
的体积的最大值.
【题目】某电视台举行文艺比赛,并通过网络对比赛进行直播.比赛现场有5名专家评委给每位参赛选手评分,场外观众可以通过网络给每位参赛选手评分.每位选手的最终得分由专家评分和观众评分确定.某选手参与比赛后,现场专家评分情况如表;场外有数万名观众参与评分,将评分按照[7,8),[8,9),[9,10]分组,绘成频率分布直方图如图:
专家 | A | B | C | D | E |
评分 | 9.6 | 9.5 | 9.6 | 8.9 | 9.7 |
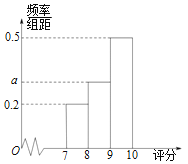
(1)求a的值,并用频率估计概率,估计某场外观众评分不小于9的概率;
(2)从5名专家中随机选取3人,X表示评分不小于9分的人数;从场外观众中随机选取3人,用频率估计概率,Y表示评分不小于9分的人数;试求E(X)与E(Y)的值;
(3)考虑以下两种方案来确定该选手的最终得分:方案一:用所有专家与观众的评分的平均数![]() 作为该选手的最终得分,方案二:分别计算专家评分的平均数
作为该选手的最终得分,方案二:分别计算专家评分的平均数![]() 和观众评分的平均数
和观众评分的平均数![]() ,用
,用![]() 作为该选手最终得分.请直接写出
作为该选手最终得分.请直接写出![]() 与
与![]() 的大小关系.
的大小关系.