题目内容
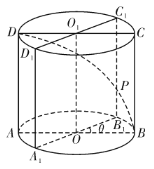
【题目】已知圆柱![]() 底面半径为1,高为
底面半径为1,高为![]() ,
,![]() 是圆柱的一个轴截面,动点
是圆柱的一个轴截面,动点![]() 从点
从点![]() 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点![]() ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线![]() 如图所示.将轴截面
如图所示.将轴截面![]() 绕着轴
绕着轴![]() 逆时针旋转
逆时针旋转![]() 后,边
后,边![]() 与曲线
与曲线![]() 相交于点
相交于点![]() .
.
(1)求曲线![]() 的长度;
的长度;
(2)当![]() 时,求点
时,求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将圆柱的一半展开,可知曲线![]() 的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,即可求得曲线
的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,即可求得曲线![]() 的长度.
的长度.
(2)当![]() 时,以底面的圆心O为原点建立空间直角坐标系.写出各个点的坐标,求得平面
时,以底面的圆心O为原点建立空间直角坐标系.写出各个点的坐标,求得平面![]() 的法向量,即可求得点
的法向量,即可求得点![]() 到平面
到平面![]() 的距离.
的距离.
(1)曲线![]() 的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,
的长度为矩形的对角线长度.其中矩形的宽为圆柱的高,长为底面的半圆长,
其中![]() ,底面的半圆长为
,底面的半圆长为![]()
∴![]() 的长为
的长为![]()
(2)当![]() 时,建立如图所示的空间直角坐标系:
时,建立如图所示的空间直角坐标系:

则有![]() 、
、![]() 、
、![]() 、
、![]() ,
,
所以![]() 、
、![]() 、
、![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,代入可得
,代入可得 ,
,
令![]() ,得
,得![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为 .
.

练习册系列答案
相关题目