题目内容
4.已知z=$\frac{{{{(1+i)}^2}}}{2+3i}$(i是虚数单位),则z的共轭复数对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的代数形式混合运算化简复数,求出复数的对应点的坐标即可.
解答 解:z=$\frac{{{{(1+i)}^2}}}{2+3i}$=$\frac{2i}{2+3i}$=$\frac{2i(2-3i)}{13}$=$\frac{6}{13}$+$\frac{4}{13}$i,
复数的对应点的坐标($\frac{6}{13}$,$\frac{4}{13}$)在第一象限.共轭复数对应点为:($\frac{6}{13}$,-$\frac{4}{13}$)在第四象限.
故选:D.
点评 本题考查复数的代数形式混合运算,复数的几何意义,是基础题.

练习册系列答案
相关题目
13.已知A、B、C为△ABC的三个内角,向量$\overrightarrow{m}$满足|$\overrightarrow{m}$|=$\frac{\sqrt{6}}{2}$,且$\overrightarrow{m}$=($\sqrt{2}$sin$\frac{B+C}{2}$,cos$\frac{B-C}{2}$),若A最大时,动点P使得|$\overrightarrow{PB}$|、|$\overrightarrow{BC}$|、|$\overrightarrow{PC}$|成等差数列,则$\frac{|\overrightarrow{PA}|}{|\overrightarrow{BC}|}$的最大值是( )
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
9.调查表明,市民对城市的居住满意度与该城市环境质量、城市建设、物价与收入的满意度有极强的相关性,现将这三项的满意度指标分别记为x、y、z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标ω=x+y+z的值评定居民对城市的居住满意度等级:若ω≥4,则居住满意度为一级;若2≤?≤3,则居住满意度为二级;若0≤?≤1,则居住满意度为三级,为了解某城市居民对该城市的居住满意度,研究人员从此城市居民中随机抽取10人进行调查,得到如下结果:
(Ⅰ)若该城市有200万人常住人口,试估计该城市居民中居住满意度为三级的人数是多少?
(Ⅱ)从居住满意度为一级的被调查者中随机抽取两人,这两人的居住满意度指标ω均为4的概率是多少?
| 人员编号 | 1 | 2 | 3 | 4 | 5 |
| (x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,1,1) | (1,2,1) |
| 人员编号 | 6 | 7 | 8 | 9 | 10 |
| (x,y,z) | (1,2,2) | (1,1,1) | (1,2,2) | (1,0,0) | (1,1,1) |
(Ⅱ)从居住满意度为一级的被调查者中随机抽取两人,这两人的居住满意度指标ω均为4的概率是多少?
16.执行如图所示程序框图,输出的a=( )


| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
13.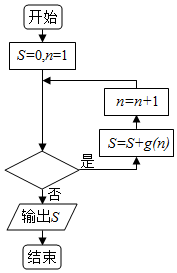 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )
 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=-1处取得极大值,记g(x)=$\frac{1}{f′(x)}$.在如图所示的程序框图中,若输出的结果S=$\frac{2016}{2017}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2016? | B. | n≤2017? | C. | n>2016? | D. | n>2017? |