题目内容
设椭圆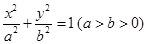 的左右顶点分别为
的左右顶点分别为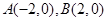 ,离心率
,离心率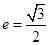 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且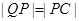 .
.
(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线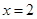 交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
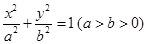 的左右顶点分别为
的左右顶点分别为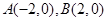 ,离心率
,离心率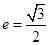 .过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且
.过该椭圆上任一点P作PQ⊥x轴,垂足为Q,点C在QP的延长线上,且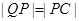 .
.(1)求椭圆的方程;
(2)求动点C的轨迹E的方程;
(3)设直线AC(C点不同于A,B)与直线
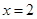 交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.
交于点R,D为线段RB的中点,试判断直线CD与曲线E的位置关系,并证明你的结论.(1) ;(2)
;(2)  ;(3) 直线
;(3) 直线 与圆
与圆 相切,证明见解析.
相切,证明见解析.
 ;(2)
;(2)  ;(3) 直线
;(3) 直线 与圆
与圆 相切,证明见解析.
相切,证明见解析.试题分析:(1)要求椭圆的方程,就要知道a,b,由点A知道a=2,由离心率可求得c,由a2=b2+c2进而求出b=1;(2)求动点的轨迹方程,首先设
 ,
, ,利用
,利用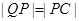 用C点表示P点坐标,
用C点表示P点坐标, ,代入椭圆方程,从而得到动点C的轨迹;(3)直线与圆的位置关系有三种,相交,相切,相离,判断的方法是圆心到直线的距离与半径的关系,如果⊙O的半径为r,圆心O到直线l的距离为d,那么:直线l与⊙O相交
,代入椭圆方程,从而得到动点C的轨迹;(3)直线与圆的位置关系有三种,相交,相切,相离,判断的方法是圆心到直线的距离与半径的关系,如果⊙O的半径为r,圆心O到直线l的距离为d,那么:直线l与⊙O相交 d<r;直线l与⊙O相切
d<r;直线l与⊙O相切 d=r;直线l与⊙O相离
d=r;直线l与⊙O相离 d>r;求出圆心到直线的距离后和半径进行比较,可得直线与圆的位置关系.
d>r;求出圆心到直线的距离后和半径进行比较,可得直线与圆的位置关系.试题解析:(1)由题意可得
 ,
, ,
,∴
 ,
,∴
 ,
,∴椭圆的方程为
 .
.(2)设
 ,
, ,由题意得
,由题意得 ,即
,即 ,
,又
 ,代入得
,代入得 ,即
,即 .
.即动点
 的轨迹
的轨迹 的方程为
的方程为 .
.(3)设
 ,点
,点 的坐标为
的坐标为 ,
,∵
 三点共线,
三点共线,∴
 ,
,而
 ,
, ,
,则
 ,
,∴
 ,
, ∴点
 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,
,∴直线
 的斜率为
的斜率为 ,
,而
 ,
,∴
 ,
,∴
 ,
,∴直线
 的方程为
的方程为 ,
,化简得
 ,
,∴圆心
 到直线
到直线 的距离
的距离 ,
,∴直线
 与圆
与圆 相切.
相切.
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
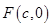 是椭圆
是椭圆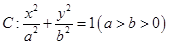 的右焦点;圆
的右焦点;圆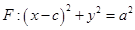 与
与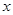 轴交于
轴交于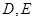 两点,其中
两点,其中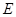 是椭圆
是椭圆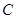 的左焦点.
的左焦点.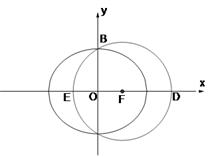
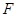 与
与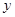 轴的正半轴的交点为
轴的正半轴的交点为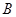 ,点
,点 是点
是点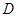 关于
关于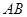 与圆
与圆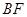 与圆
与圆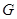 ,若
,若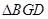 的面积为
的面积为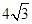 ,求椭圆
,求椭圆 .设圆O上到直线l的距离等于1的点的个数为k,则k=________.
.设圆O上到直线l的距离等于1的点的个数为k,则k=________. 与圆
与圆 的位置关系是( )
的位置关系是( ) 的渐近线与圆
的渐近线与圆 有公共点,则该双曲线离心率的取值范围是__________.
有公共点,则该双曲线离心率的取值范围是__________. 是圆
是圆 的切线,切点为
的切线,切点为 ,
, .
. 是圆
是圆 与圆
与圆 ,
, ,则圆
,则圆 .
. 及直线
及直线 ,则圆心
,则圆心 到直线
到直线 距离为____.
距离为____. (
( 为参数),直线
为参数),直线 的极坐标方程为
的极坐标方程为 .则直线与曲线C的位置关系为 .
.则直线与曲线C的位置关系为 . 所得弦长为2,则圆心C的轨迹方程为( )
所得弦长为2,则圆心C的轨迹方程为( )


