题目内容
已知函数 是
是 上的偶函数,满足
上的偶函数,满足 ,当
,当 时,
时,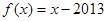 ,则( )
,则( )
A. B.
B.
C.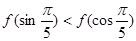 D.
D.
D
解析试题分析:因为对任意的x满足 ,所以函数f(x)的周期为2;所以当
,所以函数f(x)的周期为2;所以当 ,
,
又 ,所以
,所以 。
。
考点:函数的奇偶性;函数的单调性。
点评:利用函数的奇偶性求函数的解析式,此类问题的一般做法是:①“求谁设谁”?即在哪个区间求解析式,x就设在哪个区间内;②要利用已知区间的解析式进行代入;③利用f(x)的奇偶性写出-f(x)或f(-x),从而解出f(x)。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
函数 的零点所在的大致区间是
的零点所在的大致区间是
| A.(6,7) | B.(7,8) | C.(8,9) | D.(9,10) |
已知 ,若函数
,若函数 ,则
,则 的
的
根的个数最多有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 ,都有
,都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D.1 |
函数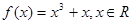 ,当
,当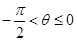 时,
时,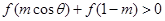 恒成立,则实数
恒成立,则实数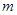 的取值范围是( )
的取值范围是( )
A.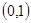 | B.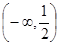 | C.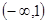 | D.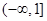 |
函数 的定义域是
的定义域是
A. | B. | C. | D. |
定义在 上的函数
上的函数 ,如果存在函数
,如果存在函数 ,使得
,使得 对一切实数
对一切实数 都成立,则称
都成立,则称 是函数
是函数 的一个“亲密函数”,现有如下的命题:
的一个“亲密函数”,现有如下的命题:
(1)对于给定的函数 ,其“亲密函数”有可能不存在,也可能有无数个;
,其“亲密函数”有可能不存在,也可能有无数个;
(2) 是
是 的一个“亲密函数”;
的一个“亲密函数”;
(3)定义域与值域都是 的函数
的函数 不存在“亲密函数”。
不存在“亲密函数”。
其中正确的命题是( )
| A.(1) | B.(2) | C.(1)(2) | D.(1)(3) |
下列函数 中,满足“对任意
中,满足“对任意 ,
,
 ,当
,当 时,都有
时,都有 ,的是( )
,的是( )
A. | B. | C. | D. |
已知以 为周期的函数
为周期的函数 ,其中
,其中 。若方程
。若方程 恰有5个实数解,则
恰有5个实数解,则 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |