题目内容
函数数列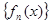 满足:
满足: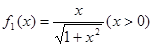 ,
,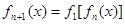
(1)求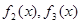 ;
;
(2)猜想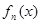 的表达式,并证明你的结论.
的表达式,并证明你的结论.
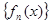 满足:
满足: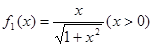 ,
,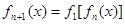
(1)求
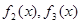 ;
;(2)猜想
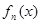 的表达式,并证明你的结论.
的表达式,并证明你的结论.(1)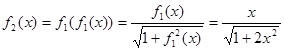
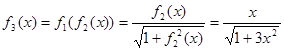
(2)猜想: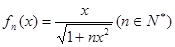
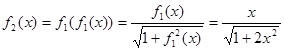
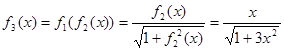
(2)猜想:
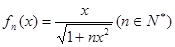
(1)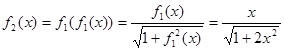
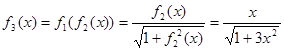
(2)猜想: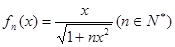
下面用数学归纳法证明:
①当n=1时,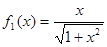 ,已知,显然成立
,已知,显然成立
②假设当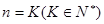 时,猜想成立,即
时,猜想成立,即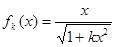
则当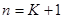 时,
时,
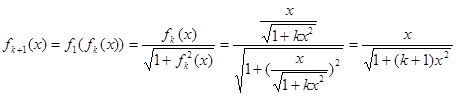
即对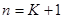 时,猜想也成立.
时,猜想也成立.
由①②可得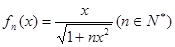 成立
成立
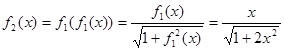
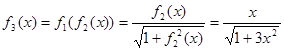
(2)猜想:
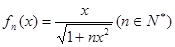
下面用数学归纳法证明:
①当n=1时,
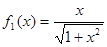 ,已知,显然成立
,已知,显然成立②假设当
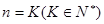 时,猜想成立,即
时,猜想成立,即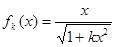
则当
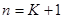 时,
时,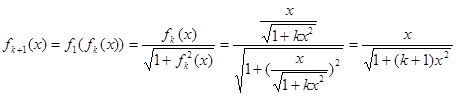
即对
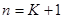 时,猜想也成立.
时,猜想也成立.由①②可得
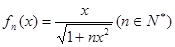 成立
成立
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
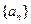 满足
满足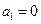 ,
,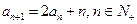 .
.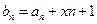 ,是否存在实数
,是否存在实数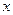 ,使得
,使得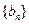 是等比数列;
是等比数列;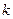 ,使得
,使得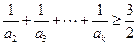 成立?若存在,求出
成立?若存在,求出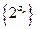 的前n项和Sn.
的前n项和Sn.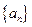 为等差数列,公差
为等差数列,公差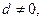
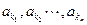 恰为等比数列,若
恰为等比数列,若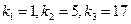 ,则
,则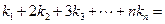 __ ▲ __.
__ ▲ __.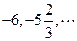 .的前
.的前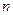 项和为
项和为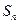 ,使
,使 中,
中, ,则它的前10项和为( )
,则它的前10项和为( )

 .
.




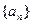 满足
满足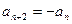 ,且
,且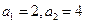 ,则该数列的前509项的和为 .
,则该数列的前509项的和为 .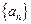 中,
中,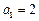 ,
,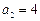 ,对于函数
,对于函数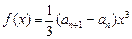
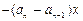 (其中
(其中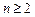 ,
,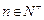 ),有
),有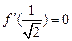 ,则数列
,则数列