题目内容
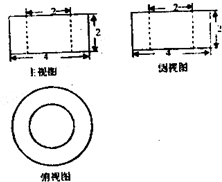
某几何体的三视图如图所示，则该几何体的体积为 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由已知的三视图可得：该几何体是一个以俯视图为底面的锥体，分别求出底面面积和高，代入锥体体积公式，可得答案．
解答：
解：由已知的三视图可得：该几何体是一个以俯视图为底面的锥体，
其底面面积S=
×4×2=4，
高h=2，
故体积V=
Sh=
×4×2=
，
故答案为：
；
其底面面积S=
| 1 |
| 2 |
高h=2，
故体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
点评：本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
冲刺100分1号卷系列答案
相关题目
已知函数f（x）是定义在R上的奇函数f（1）=0，当x＞0时，有
＞0成立，则不等式f（x）＞0的解集是（ ）
| xf′(x)-f(x) |
| x2 |
| A、（1，+∞） |
| B、（-1，0） |
| C、（-1，0）∪（1，+∞） |
| D、（-∞，-1）∪（1，+∞） |
已知梯形ABCD中，AB∥CD，∠B=
，DC=2AB=2BC=2，以对角线AC为旋转轴旋转一周得到的几何体的表面积为（ ）
| π |
| 2 |
A、2（1+
| ||||
B、2
| ||||
C、
| ||||
D、（3+2
|
若一个几何体的三视图如图所示，则其体积为（ ）
| A、5π | B、6π | C、7π | D、8π |
已知函数f（x）为偶函数，且f（2+x）=f（2-x），当-2≤x≤0时，f（x）=2x，则f（2010）=（ ）
| A、2010 | ||
B、
| ||
| C、-4 | ||
| D、4 |