题目内容
某种产品有一等品、二等品、次品三个等级,其中一等品和二等品都是正品.现有6件该产品,从中随机抽取2件来进行检测.
(1)若6件产品中有一等品3件、二等品2件、次品1件.
①抽检的2件产品全是一等品的概率是多少?
②抽检的2件产品中恰有1件是二等品的概率是多少?
(2)如果抽检的2件产品中至多有1件是次品的概率不小于 ,则6件产品中次品最多有多少件?
,则6件产品中次品最多有多少件?
解:(1)记“抽取的2件产品全是一等品”为事件 ,
,
“抽取的2件产品中恰有1件是二等品”为事件 .
.
从6件产品中随机抽取2件,有5+4+3+2+1=15种抽法.
从3件一等品中随机抽取2件,有2+1=3种抽法,故 ;
;
抽取的2件产品中恰有1件是二等品的抽法有8种,故 .
.
(2)设6件产品中有 件次品
件次品 ,
, N).
N).
当 或
或 时,抽检的2件产品中至多有1件是次品的概率等于1;
时,抽检的2件产品中至多有1件是次品的概率等于1;
当 时,则抽检的2件产品中至多有1件是次品的概率为
时,则抽检的2件产品中至多有1件是次品的概率为 ;
;
当 时,则抽检的2件产品中至多有1件是次品的概率为
时,则抽检的2件产品中至多有1件是次品的概率为 ;
;
当 时,则抽检的2件产品中至多有1件是次品的概率为
时,则抽检的2件产品中至多有1件是次品的概率为 ;
;
当 时,则抽检的2件产品中至多有1件是次品的概率为
时,则抽检的2件产品中至多有1件是次品的概率为 .
.
于是, 的最大值等于3.
的最大值等于3.
答:抽检的2件产品全是一等品的概率是 ;抽检的2件产品中恰有1件是二等品的概率是
;抽检的2件产品中恰有1件是二等品的概率是 .若抽检的2件产品中至多有1件次品的概率不小于
.若抽检的2件产品中至多有1件次品的概率不小于 ,则6件产品中次品最多有3件.
,则6件产品中次品最多有3件.

练习册系列答案
相关题目
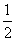 B.-
B.- D.-
D.- 的最小值等于
的最小值等于 B.
B. C.
C. D.
D.
 的扇形内画一个内切圆,若向扇形内任投一点,则该点落在该内切圆内的概率是 .
的扇形内画一个内切圆,若向扇形内任投一点,则该点落在该内切圆内的概率是 .
 ,那么BC= .
,那么BC= . ,髙二 1000人,高三1050人.现要调查该校学生
,髙二 1000人,高三1050人.现要调查该校学生 的视力状况,考虑采用分层抽样的方法,抽取容量为60的样本,则应从高三年级中抽取的人数为
的视力状况,考虑采用分层抽样的方法,抽取容量为60的样本,则应从高三年级中抽取的人数为  的
的 内任投一点
内任投一点 ,则随机事件“
,则随机事件“ 的面积大于
的面积大于 ”的
”的 ,则
,则 等于( )
等于( ) C.
C. D.
D.
 的前
的前 项和为
项和为 ,且
,且 ,则该数列的公差
,则该数列的公差 ( )
( )