题目内容
已知{an}为正项等比数列,且a2,
a3,a1成等比数列,则
= .
| 1 |
| 2 |
| a3+a4 |
| a4+a5 |
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:由题意和等比数列的通项公式可得q的方程,解方程可得q,而
=
,代值计算可得.
| a3+a4 |
| a4+a5 |
| 1 |
| q |
解答:
解:设正项等比数列{an}的公比为q,(q>0),
∵a2,
a3,a1成等比数列,
∴(
a3)2=a2a1,∴a32=4a2a1,
∴a12q3=4a12q,解得q=2,
∴
=
=
=
,
故答案为:
.
∵a2,
| 1 |
| 2 |
∴(
| 1 |
| 2 |
∴a12q3=4a12q,解得q=2,
∴
| a3+a4 |
| a4+a5 |
| a3+a4 |
| (a3+a4)q |
| 1 |
| q |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查等比数列的通项公式,属基础题.

练习册系列答案
相关题目
为测量地面上B,C两点间的距离,在高100m的建筑物顶部选点A,在A出测得点B,C的俯角分别为30°和45°(B,C与建筑物底部在同一水平面上),且∠BAC=45°,则B,C之间的距离为( )
| A、100m | ||
B、100
| ||
C、100
| ||
| D、200m |
若双曲线
-
=1(a>0,b>0)的下焦点是F,点A,B分别是双曲线的两个虚轴端点,且向量
与
的夹角θ的余弦值cosθ=
,则该双曲线一条渐近线的倾斜角为( )
| y2 |
| a2 |
| x2 |
| b2 |
| FA |
| FB |
| 1 |
| 3 |
| A、30° | B、60° |
| C、90° | D、135° |
已知a∈R,b∈R+,e为自然数的底数,则[
ea-ln(2b)]2+(a-b)2的最小值为( )
| 1 |
| 2 |
| A、(1-ln2)2 | ||
| B、2(1-ln2)2 | ||
| C、1+ln2 | ||
D、
|
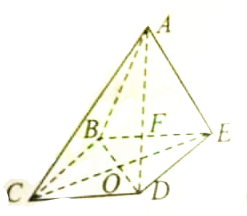 如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;
如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;